第一节基本用法

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(10)
y = x * 2 + 4
plt.plot(x, y)
plt.show()

注意要点：

首先导入画图工具类，和numpy计算包产生x,y数据
plt.plot()绘制函数图像，每一个plot()都是对应的一个图形。
最后通过plt.show()将图像展示出来

第二节 figure图像

import matplotlib.pyplot as plt
import numpy as np
import math


def drawcurve(x, y):
    return math.pow(x,y)


def drawcircle(x, r):
    return math.sqrt(r**2 - x**2), - math.sqrt(r**2 - x**2)


plt.figure('Red Dotted Curve')
x = np.linspace(-5, 5, 100)
convert = np.vectorize(drawcurve)
y = convert(x, 2)+convert(x, 3)
plt.plot(x,y, color='red', linewidth='2', linestyle='--')

plt.figure('Circle')
x = np.linspace(-5, 5,1000)
convertCircle = np.vectorize(drawcircle)
positive, negative = convertCircle(x, 5)
plt.plot(x, positive, color='blue', linewidth='3', linestyle='-')
plt.plot(x, negative, color='blue', linewidth='3', linestyle='-')

plt.show()

注意要点：

首先导入画图工具类，和numpy计算包产生x,y数据
定义两个函数，drawcurve和drawcircle。分别对两个函数进行了向量化操作。
plt.figure()会单独开辟出一个画图的窗体，每个figure()都是独立的。

plt.figure 调用方法：

plt.figure(num=None, figsize=None, dpi=None, 
		   facecolor=None, edgecolor=None, frameon=True, 
		   FigureClass=<class 'matplotlib.figure.Figure'>, 
		   clear=False, **kwargs)

参考文档：matplotlib.pyplot.figure

参数说明：

num 当给它一个数字时，就作为画板的编号，相当于 ID 号；当给它一个字符串时，就作为画板的名称
figsize 画板的宽、高，单位为英寸 (2.5cm)
dpi 指定在该画板上绘制的图像的分辨率，即每英寸多少个像素
facecolor 画板的背景颜色
edgecolor 画板的边框颜色
frameon 是否显示边框

第三节设置坐标轴

还是根据上一个画曲线和画圆的例子来看，我们的横轴和数轴的竖轴不是成比例的。所有导致画出来的图型在横轴或竖轴上都有些拉伸，因此我们可以设置在横轴和竖轴上的刻度范围。

import matplotlib.pyplot as plt
import numpy as np

#定义一个图像
plt.figure('Demo of xlim,ylim')

x = np.linspace(-5, 5, 100)
y = x**3

#设置x轴和y轴的刻度范围
plt.xlim((-5, 5))
plt.ylim((-5, 5))

#设置x轴和y轴的标签
plt.xlabel('x = [-5,5]')
plt.ylabel('y')

plt.plot(x, y, color='red', linewidth='2', linestyle='--')
plt.show()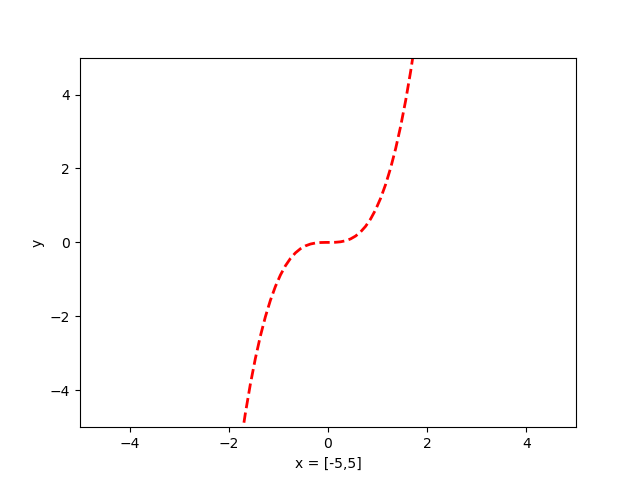

x轴和y轴都限制在了【-5， 5】的范围，这样的图像画出来才更符合我们平时看到的图像，对吧！

但是x轴和y轴的刻度是每两个数来显示的，我们可以自定义显示的刻度，下面我们来设置下坐标轴的刻度值，我们将设定为每一个显示一个刻度：

...

#设置x轴和y轴的标签
plt.xlabel('x = [-3,3]')
plt.ylabel('y')

#设置x轴和y轴的刻度
plt.xticks(np.arange(-3, 4))
plt.yticks(np.arange(-3, 4))

...

这样看起来是不是更好了，下面我们把坐标轴移动到中心：

...

#设置x轴和y轴的刻度
plt.xticks(np.arange(-3, 4))
plt.yticks(np.arange(-3, 4))

#设置坐标轴
ax = plt.gca()
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))

...

这里介绍一下代码：

plt.plot()实际上会通过plt.gca()获得当前的Axes对象ax，然后再调用ax.plot()方法实现真正的绘图。

首先搞清楚了一直以来的疑惑（借用官方文档的一幅图说明）：Figure，Axes，Axis 这三个是什么关系。

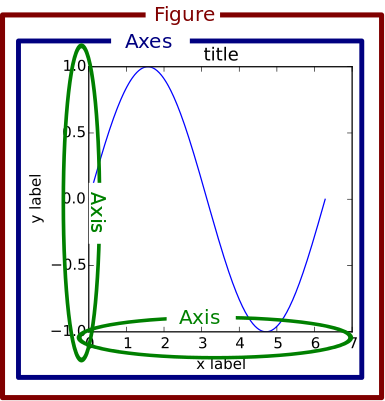
Figure：红色的外框，其实可以把它理解为一个大画板，我们所有的内容都会画在这个“画板”上
Axes：蓝色的内框，有人这么解释：

Axis 指 x、y 坐标轴等（如果有三维那就还有 z 轴），代表的是 “坐标轴”。而 Axes 在英文里是 Axis 的复数形式，也就是说 axes 代表的其实是 figure 当中的一套坐标轴。之所以说一套而不是两个坐标轴，是因为如果你画三维的图，axes 就代表 3 根坐标轴了。所以，在一个 figure 当中，每添加一次 subplot ，其实就是添加了一套坐标轴，也就是添加了一个 axes，放在二维坐标里就是你添加了两根坐标轴，分别是 x 轴和 y 轴。所以当你只画一个图的时候，plt.xxx 与 ax.xxx 其实都是作用在相同的图上的。

说话的方式简单点… 要不就把 Axes 理解为子图（画布）吧，一张大画板 figure 上可以有一个或多个子图（画布）Axes，当只有一个 axes 时，plt.plot() 和 ax.plot() 自然就作用的是同一张图了！

Axis：绿色的横纵坐标轴，这个才是正儿八经的坐标轴！

第四节绘制子图

类似于下面这样，定义 4 个 subplot，自然就有 4 个 Axes：

总结一下： figure 是作图时给你的一个大画板，而 axes 是在这个画板上的很多幅画布（子图），绘制的所有图都在画布（axes）上。比如上面的漫画布局，就可以用：

plt.figure()
plt.gcf().subplots(2,2)

来完成。其中 .gcf() 的作用是获取当前 figure，即 get current figure。另外对应的 .gca() 就是获取当前 axes，即 get current axes。

import matplotlib.pyplot as plt
import numpy as np


x = np.linspace(0, 5, 100)

#将figure分为4个子图（Axes)
fig, axes = plt.subplots(2, 2)
ax1 = axes[0, 0]    # 根据索引［0，0］从Axes对象数组中获取第1个子图
ax2 = axes[0, 1]    # 根据索引［0，1］从Axes对象数组中获取第2个子图
ax3 = axes[1, 0]    # 根据索引［1，0］从Axes对象数组中获取第3个子图
ax4 = axes[1, 1]    # 根据索引［1，1］从Axes对象数组中获取第4个子图

ax1.plot(x, x**2)
ax2.plot(x, -x)
ax3.plot(x, np.sqrt(x))
ax4.plot(x, np.log(x))

plt.show()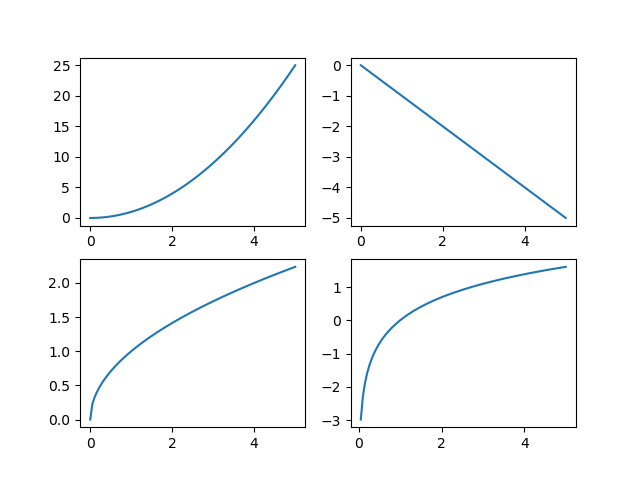

我们根据之前所学丰富一下坐标轴信息：

import matplotlib.pyplot as plt
import numpy as np
import math as m

x = np.linspace(0.1, 5, 100)

#将figure分为4个子图（Axes)
fig, axes = plt.subplots(2, 2)
ax1 = axes[0, 0]    # 根据索引［0，0］从Axes对象数组中获取第1个子图
ax2 = axes[0, 1]    # 根据索引［0，1］从Axes对象数组中获取第2个子图
ax3 = axes[1, 0]    # 根据索引［1，0］从Axes对象数组中获取第3个子图
ax4 = axes[1, 1]    # 根据索引［1，1］从Axes对象数组中获取第4个子图

#ax1的坐标设置
ax1.set_title(r'$y=x^2$')
ax1.set_xlim((0, 5))
ax1.set_ylim((0, 25))
ax1.spines['top'].set_color('none')
ax1.spines['right'].set_color('none')
ax1.plot(x, x**2)


#ax2的坐标设置
ax2.spines['right'].set_color('none')
ax2.spines['bottom'].set_color('none')
ax2.xaxis.set_ticks_position('top')
ax2.yaxis.set_ticks_position('left')
ax2.spines['top'].set_position(('data', 0))
ax2.spines['left'].set_position(('data', 0))
ax2.set_title(r'$y=-x$')
ax2.set_xticks([0, 1, 2, 3, 4, 5])
ax2.plot(x, -x)


#ax3的坐标设置
ax3.set_title(r'$y=\sqrt{x}$')
ax3.set_xlim((0, 5))
ax3.spines['top'].set_color('none')
ax3.spines['right'].set_color('none')
ax3.xaxis.set_ticks([0, 1, 2, 3, 4, 5])
ax3.yaxis.set_ticks([0, 1, m.sqrt(2), m.sqrt(3), m.sqrt(4), m.sqrt(5)])
ax3.plot(x, np.sqrt(x))


#ax4的坐标设置
ax4.set_title(r'$y=log(x)$')
ax4.set_xlim((0, 5))
ax4.spines['top'].set_color('none')
ax4.spines['right'].set_color('none')
ax4.xaxis.set_ticks([0, 1, 2, 3, 4, 5])
ax4.spines['left'].set_position(('data', 0))
ax4.spines['bottom'].set_position(('data', 0))
ax4.plot(x, np.log(x))


plt.show()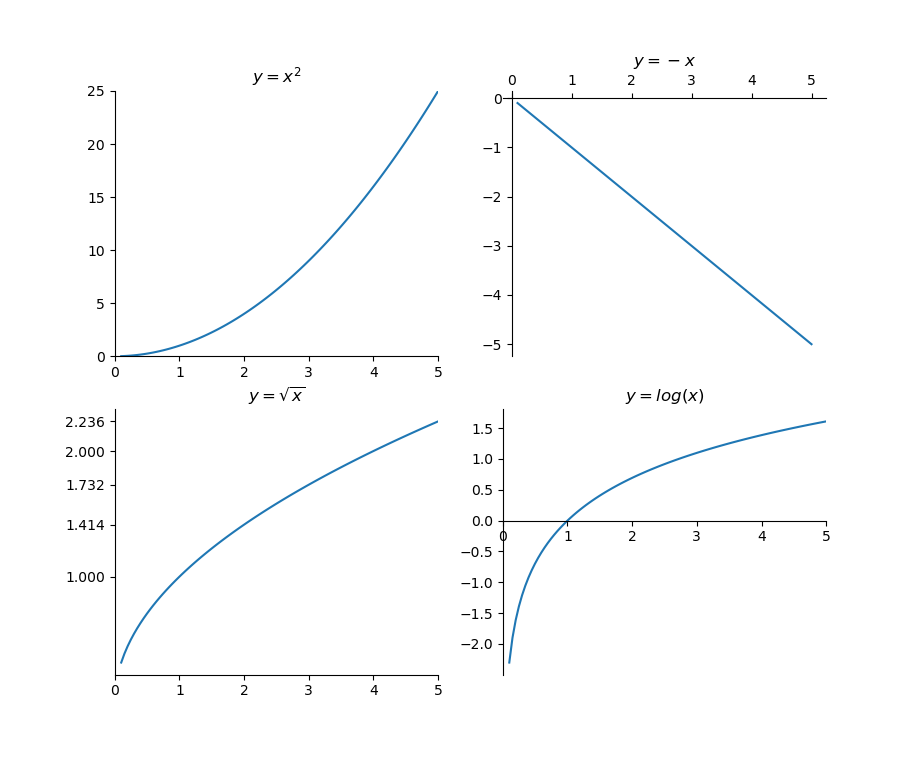

第五节 Legend图例

import matplotlib.pyplot as plt
import numpy as np
import math as m


x = np.linspace(-5, 5, 100)
y = 1 / (1 + m.e**(-x))
ax = plt.gca()

ax.set_xlim((-5, 5))
ax.set_ylim((0, 1.1))
ax.set_yticks([1])
ax.set_xticks(np.arange(-5, 6))
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['bottom'].set_position(('data', 0))

ax.plot(x, y)
ax.legend(['Sigmoid Function'], loc='best')

plt.show()

效果如下：

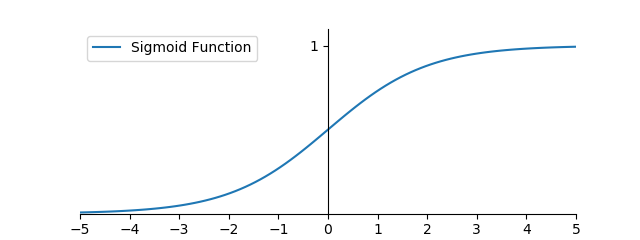
左上角出现了一个标记。

还有其他的表达方式，可以自动添加图例

ax.plot(x, y, label='Sigmoid Function')
ax.legend()

第六节 ticks标注

...
ax.spines['left'].set_position(('data', 0))
ax.spines['bottom'].set_position(('data', 0))

for label in ax.get_xticklabels()+ax.get_yticklabels():
    label.set_fontsize(10)
    label.set_bbox(dict(facecolor='yellow', edgecolor='None', alpha=0.7))

ax.plot(x, y, label='Sigmoid Function')
...

这样就在刻度上画出了一个矩形，改变了样式。

第七节散点图

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"C:\Windows\Fonts\simhei.ttf", size=14)

X1 = np.random.normal(0, 1.5, 512)
Y1 = np.random.normal(0, 1.5, 512)
X2 = np.random.normal(5, 2, 512)
Y2 = np.random.normal(5, 2, 512)
plt.title(u'散点图示例', FontProperties=font)
plt.scatter(X1, Y1, marker='o', c='y', edgecolors='r', alpha=0.6)
plt.scatter(X2, Y2, marker='o', c='m', edgecolors='g', alpha=0.6)
plt.show()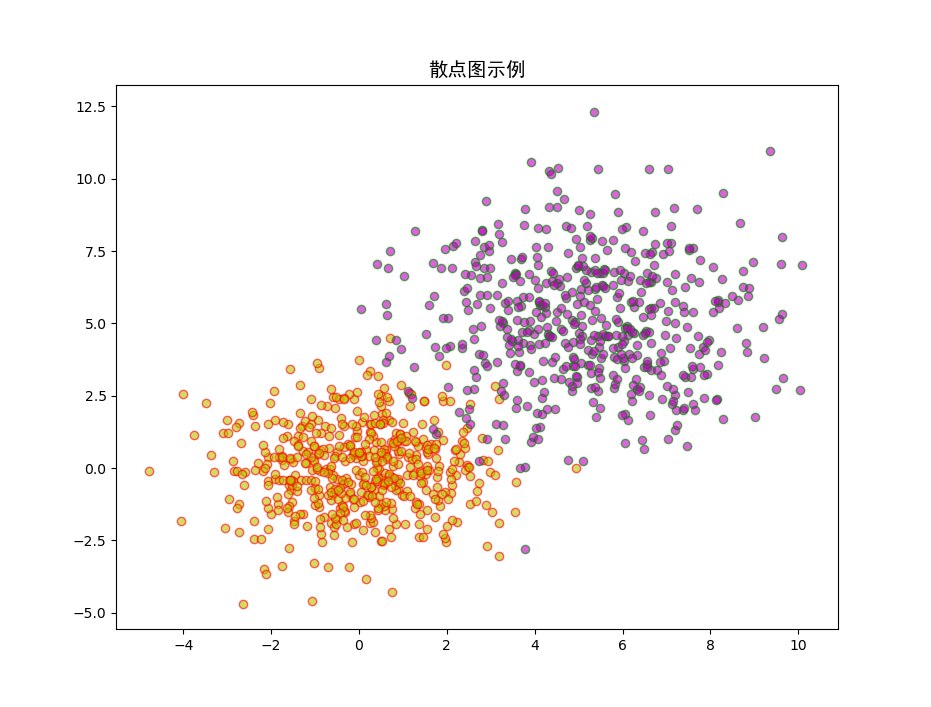

第八节 image图片

import matplotlib.pyplot as plt
import numpy as np

x = np.random.randint(155, 255, size=[255, 255])

plt.imshow(x, interpolation='nearest', cmap='bone', origin='upper')
plt.colorbar(shrink=0.9)

plt.show()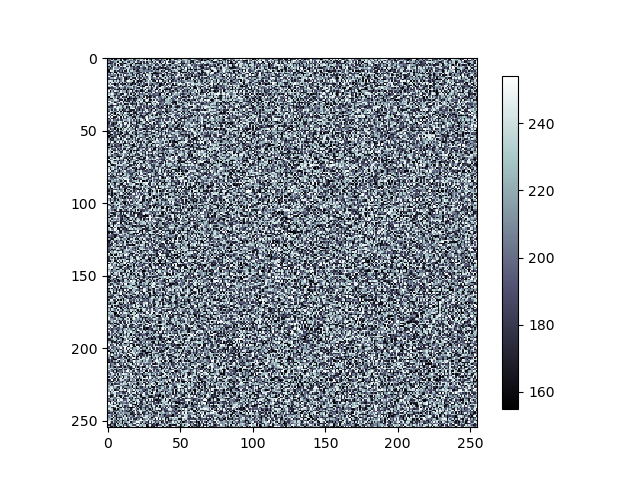

Python Matplotlib

Matplotlib

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

OpenCV快速入门上一篇

Git基本命令下一篇

Matplotlib快速入门

第一节 基本用法