题目描述

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

    1
   / \
  2   2
 / \ / \
3  4 4  3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

    1
   / \
  2   2
   \   \
   3    3

 

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

 

限制：

0 <= 节点个数 <= 1000

解题思路

这道题的做法可以采用递归实现。

对称二叉树定义： 对于树中 任意两个对称节点 LL 和 RR ，一定有：

• L.val = R.val ：即此两对称节点值相等。
• L.left.val = R.right.val：即 LL 的 左子节点 和 RR 的 右子节点 对称；
• L.right.val = R.left.val：即 LL 的 右子节点 和 RR 的 左子节点 对称。

根据以上规律，考虑从顶至底递归，判断每对节点是否对称，从而判断树是否为对称二叉树。

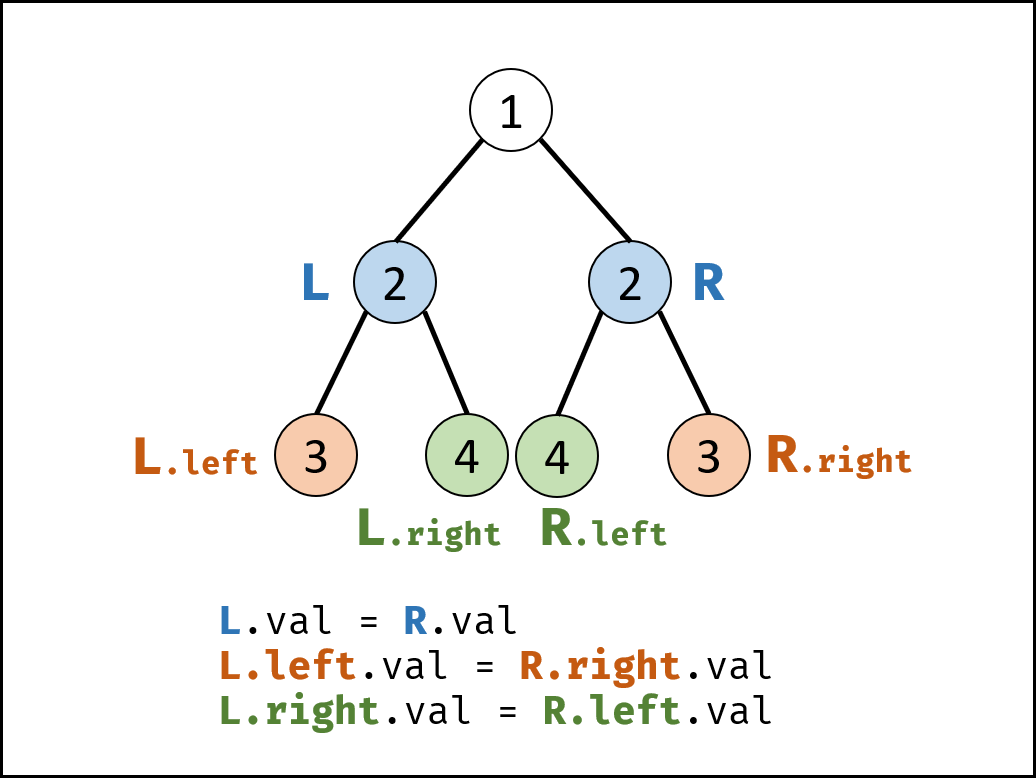
在python的语法中，我们可以用内部方法的方式来进行递归调用，代码如下：

算法实现

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        def recur(l, r):
            if not l and not r: return True
            elif not l or not r or l.val != r.val: return False
            else:
                return recur(l.left, r.right) and recur(l.right, r.left)
        return recur(root.left, root.right) if root else True

复杂度分析：

• 时间复杂度 O(N) ： 其中 N 为二叉树的节点数量，每次执行 recur() 可以判断一对节点是否对称，因此最多调用 N/2 次 recur() 方法。
• 空间复杂度 O(N) ： 最差情况下，二叉树退化为链表，系统使用O(N) 大小的栈空间。

参考文献

面试题28. 对称的二叉树