题目描述

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

• push(x) —— 将元素 x 推入栈中。
• pop() —— 删除栈顶的元素。
• top() —— 获取栈顶元素。
• getMin() —— 检索栈中的最小元素。

示例:

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

提示：

• pop、top 和 getMin 操作总是在 非空栈 上调用。

解题思路

这道题目看起来很简单，很容易将题目理解不到位。如果我们仅设置一个变量min，来存储最小值的话，那么在进行栈的pop操作的时候，会发生栈内数值得变化，从而引起最小值发生变化。因此，只定义一个变量是不够的。或许你可以选择一个集合来存储动态发生的最小值，我们考虑用栈这个结构做min的存储。

对于栈来说，如果一个元素 `a` 在入栈时，栈里有其它的元素 `b`, `c`, `d`，那么无论这个栈在之后经历了什么操作，只要 `a` 在栈中，`b`, `c`, `d` 就一定在栈中，因为在 `a` 被弹出之前，`b`, `c`, `d` 不会被弹出。

因此，在操作过程中的任意一个时刻，只要栈顶的元素是 `a`，那么我们就可以确定栈里面现在的元素一定是 `a`, `b`, `c`, `d`。

那么，我们可以在每个元素 `a` 入栈时把当前栈的最小值 `m` 存储起来。在这之后无论何时，如果栈顶元素是 `a`，我们就可以直接返回存储的最小值 `m`。

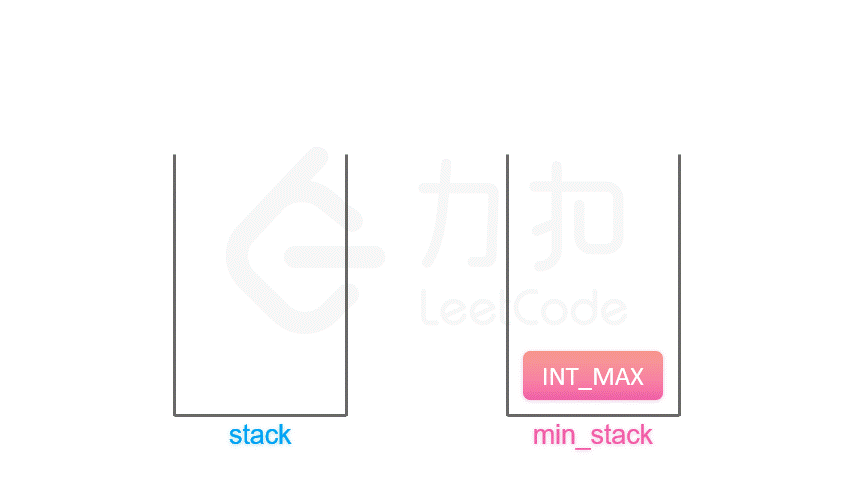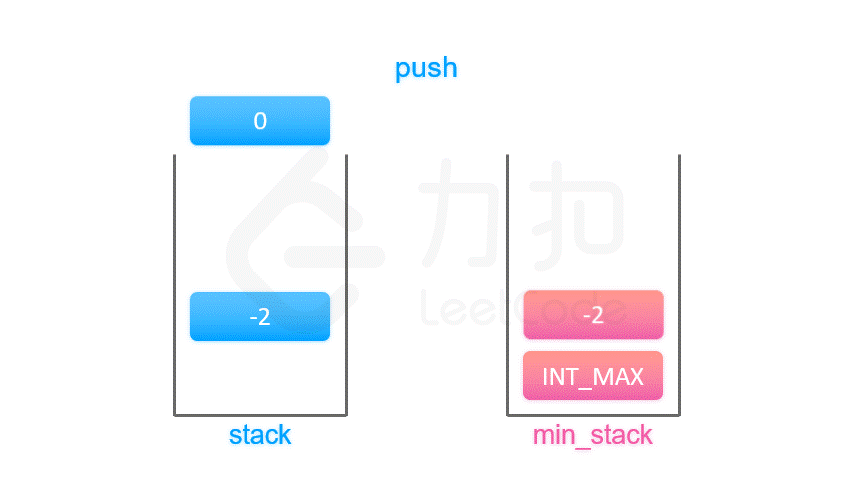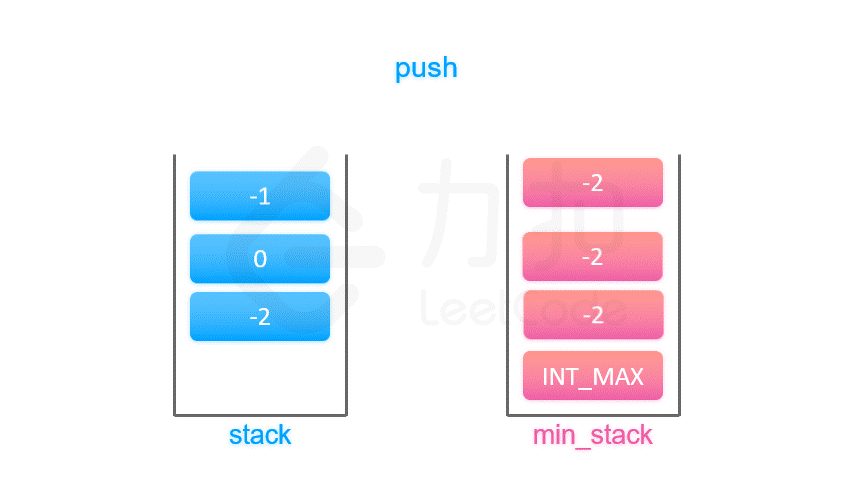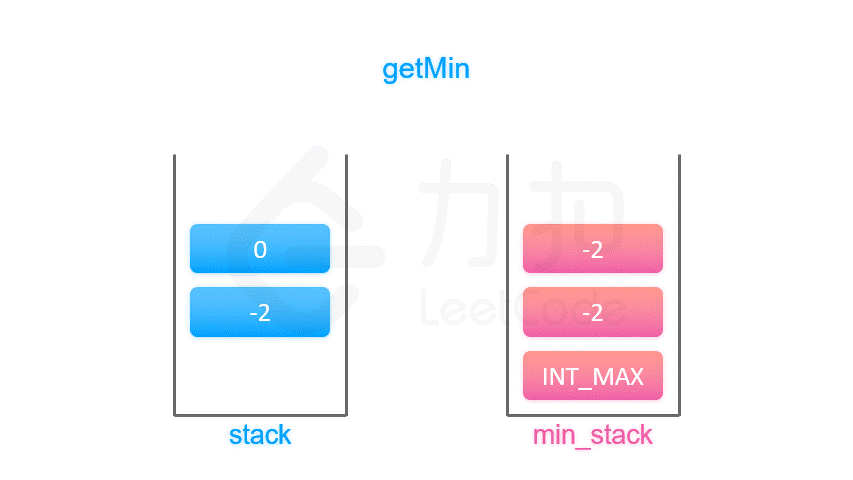
按照上面的思路，我们只需要设计一个数据结构，使得每个元素 a 与其相应的最小值 m 时刻保持一一对应。因此我们可以使用一个辅助栈，与元素栈同步插入与删除，用于存储与每个元素对应的最小值。

• 当一个元素要入栈时，我们取当前辅助栈的栈顶存储的最小值，与当前元素比较得出最小值，将这个最小值插入辅助栈中；

• 当一个元素要出栈时，我们把辅助栈的栈顶元素也一并弹出；

• 在任意一个时刻，栈内元素的最小值就存储在辅助栈的栈顶元素中。

代码实现

class MinStack:

    def __init__(self):
        self.stack = []
        self.minStack = [math.inf]

    def push(self, x: int) -> None:
        self.stack.append(x)
        self.minStack.append(min(self.minStack[-1], x))

    def pop(self) -> None:
        self.stack.pop()
        self.minStack.pop()

    def top(self) -> int:
        return self.stack[-1]

    def getMin(self) -> int:
        return self.minStack[-1]

复杂度分析

• 时间复杂度：对于题目中的所有操作，时间复杂度均为O(1)。因为栈的插入、删除与读取操作都是O(1)，我们定义的每个操作最多调用栈操作两次。

• 空间复杂度：O(n)，其中 n 为总操作数。最坏情况下，我们会连续插入 n 个元素，此时两个栈占用的空间为 O(n)。