题目描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

解题思想

我们用 f(x) 表示爬到第x级台阶的方案数，考虑最后一步可能跨了一级台阶，也可能跨了两级台阶，所以我们可以列出如下式子：

$$
f(x)=f(x−1)+f(x−2)
$$

它意味着爬到第 x 级台阶的方案数是爬到第 x−1 级台阶的方案数和爬到第 x−2 级台阶的方案数的和。很好理解，因为每次只能爬 1 级或 2 级，所以 f(x) 只能从f(x−1) 和f(x−2) 转移过来，而这里要统计方案总数，我们就需要对这两项的贡献求和。

看到这里我们不禁想起了一个与之相似的问题，那就是斐波那契数列问题！在解决这一类问题的时候我们可以选择递归和动态规划的方法实现，但是使用递归的方法牺牲比较大，时间复杂度成指数级，其中还包括了大量的重复计算。因此这里采取动态规划的思想来解决这一问题。

动态规划基本思路如下（解题四步曲）

1. 判断是否可用递归来解，可以的话进入步骤 2
2. 分析在递归的过程中是否存在大量的重复子问题
3. 采用备忘录的方式来存子问题的解以避免大量的重复计算（剪枝）
4. 改用自底向上的方式来递推，即动态规划

采用备忘录的方式来存子问题的解以避免大量的重复计算既然以上中间子问题中存在着大量的重复计算，那么我们可以把这些中间结果给缓存住（可以用哈希表缓存）

public static int climbStairs(int n) {
    if (n = 1) return1;
    if (n = 2) return2;
    if (map.get(n) != null)  {
        return map.get(n);
    }
    int result = climbStairs(n - 1) + climbStairs(n - 2);
    map.put(n, result);
    return result;
}

这么缓存之后再看我们的递归树

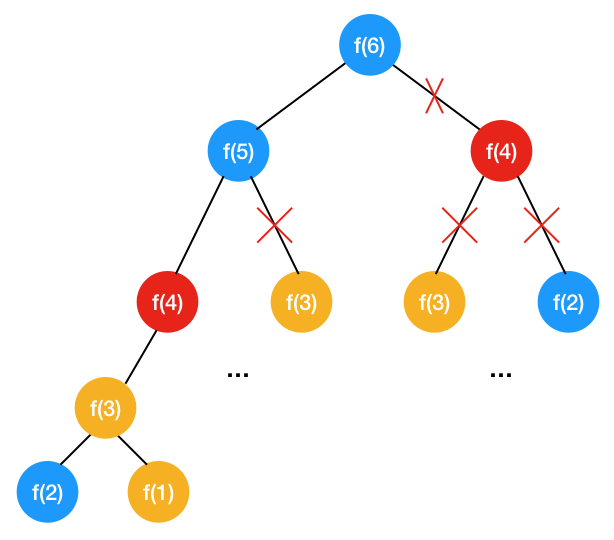
可以看到通过缓存中间的数据，做了大量地剪枝的工作，同样的f(4),f(3),f(2)，都只算一遍了,省去了大量的重复计算，问题的规模从二叉树变成了单链表（即 n），时间复杂度变成了 O(n)，不过由于哈希表缓存了所有的子问题的结果，空间复杂度是 O(n)。

改用自底向上的方式来递推，即动态规划我们注意到如下规律

f(1) = 1
f(2) = 2
f(3) = f(1) + f(2) = 3
f(4) = f(3) + f(2) = 5
....
f(n) = f(n-1) + f(n-2)

所以只要依次自底向上求出 f(3),f(4),…,自然而然地就求出了 f(n)

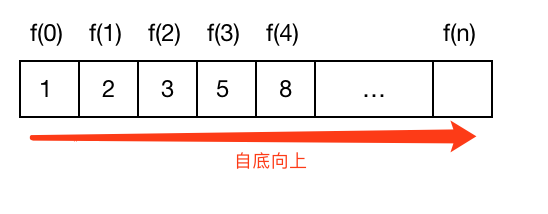
f(n) 就是定义的每个子问题的状态（DP 状态），f(n) = f(n-1) + f(n-2) 就是状态转移方程，即 f(n) 由 f(n-1), f(n-2) 这两个状态转移而来,由于每个子问题只与它前面的两个状态，所以我们只要定义三个变量，自底向上不断循环迭代即可，如下:

爬楼梯的代码实现

class Solution:
    def climbStairs(self, n: int) -> int:
        if n==1: return 1
        if n==2: return 2
        result = 0
        pre = 1
        nextt = 2
        for i in range(3, n+1):
            result = pre + nextt
            pre = nextt
            nextt = result
        return result

这样时间复杂度虽然还是O(n)，但空间复杂度只由于只定义了三个变量（result,pre,next）所以是常量 O(1)。

第 N 个泰波那契数

泰波那契序列 T_n 定义如下： 

T₀ = 0, T₁ = 1, T₂ = 1, 且在 n >= 0 的条件下 T_n+3 = T_n + T_n+1 + T_n+2

给你整数 n，请返回第 n 个泰波那契数 T_n 的值。

示例 1：

输入：n = 4
输出：4
解释：
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4

示例 2：

输入：n = 25
输出：1389537

提示：

• 0 <= n <= 37
• 答案保证是一个 32 位整数，即 answer <= 2^31 - 1。

# 解题思路

与斐波那契数列问题非常相似，但是这个问题的状态方程由三种状态组成，即：
$$
f(x)=f(x−1)+f(x−2)+f(x-3)
$$

• 如果 n < 3，答案可直接得出。

• 否则，初始化前 3 个斐波那契数字 x = 0, y = z = 1，并执行 n - 2 步循环。循环的每一步：

  令 x = y。令 y = z。令 z = x + y + z。

• 返回 z。

代码实现如下：

class Solution:
    def tribonacci(self, n: int) -> int:
        if n == 0: return 0
        if n == 1 or n == 2: return 1
        first = 0
        second = 1
        third = 1
        for i in range(n-2):
            result = first + second + third
            first = second
            second = third
            third = result
        return third

参考文献

一文学会动态规划解题技巧