回顾经典回文串链问题

一. 回文数

问题描述

判断一个整数是否是回文数。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

示例 1:

输入: 121
输出: true

示例 2:

输入: -121
输出: false
解释: 从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。

示例 3:

输入: 10
输出: false
解释: 从右向左读, 为 01 。因此它不是一个回文数。

解题思路

在这道题中，我们可以借助列表的反转方法来判断数字是否是一个回文数字。首先，由于回文串的对称性，负数一定不是回文数，那么我们只需对正数进行字符串转换。之后将字符串放到list中，使用reverse方法来判断反转之后的list和原list是否相同。若相同表示是回文数字，否则不是回文数字。

这种方法的一个缺点就是另外开辟了新的数组空间，空间复杂度偏高。

另外一种做法就是通过取整和取余操作获取整数中对应的数字进行比较。举个例子：1221 这个数字。通过计算 1221 / 1000， 得首位1；通过计算 1221 % 10， 可得末位 1；进行比较；再将 22 取出来继续比较

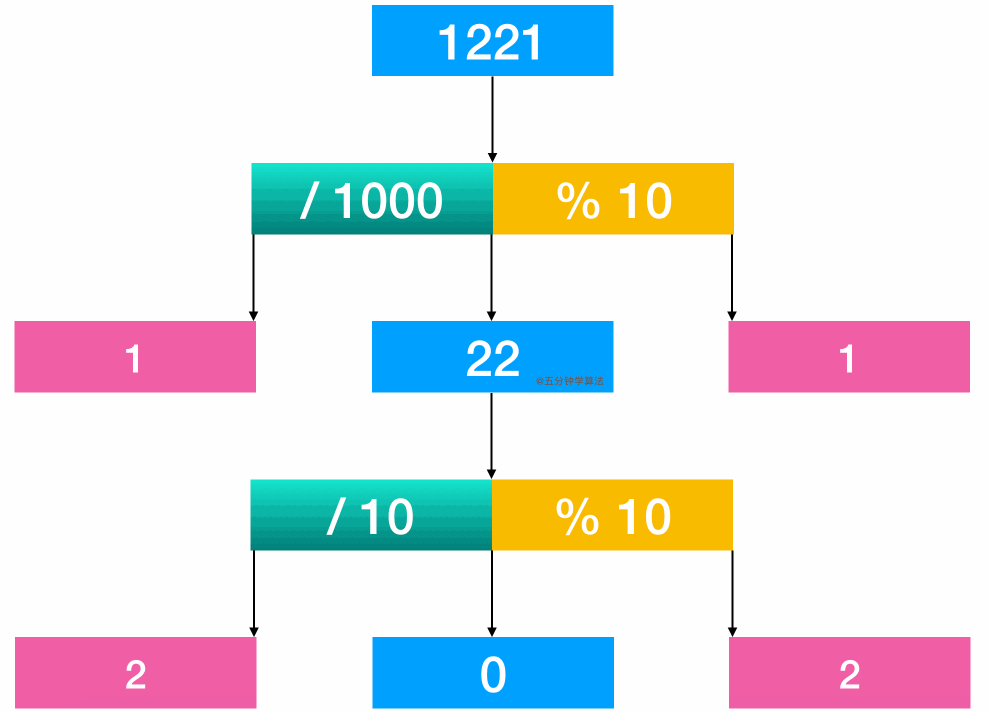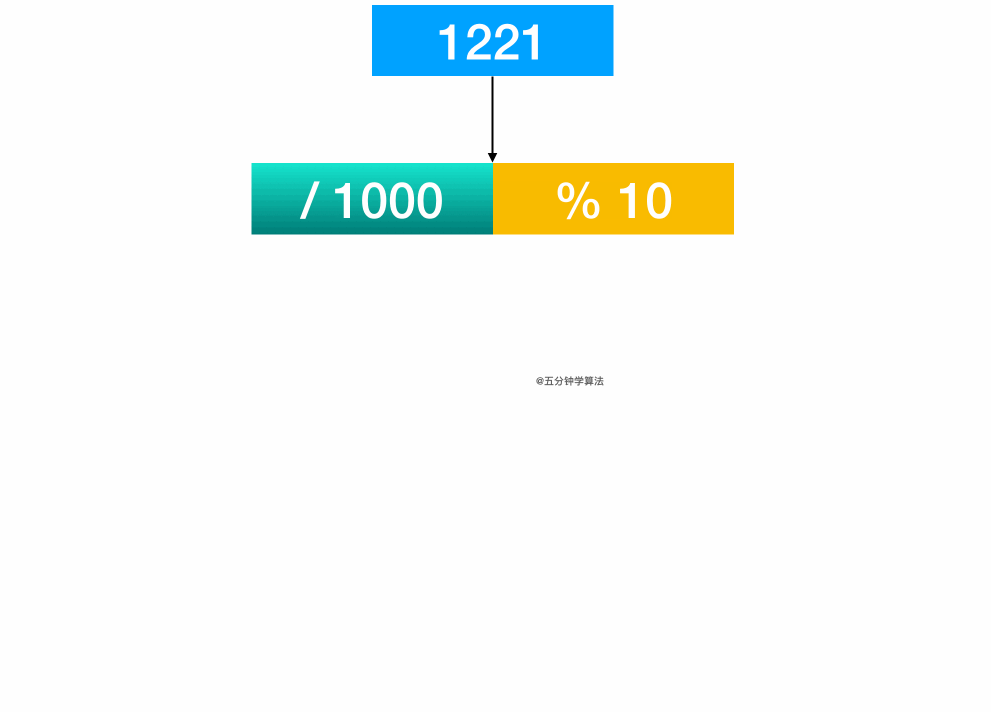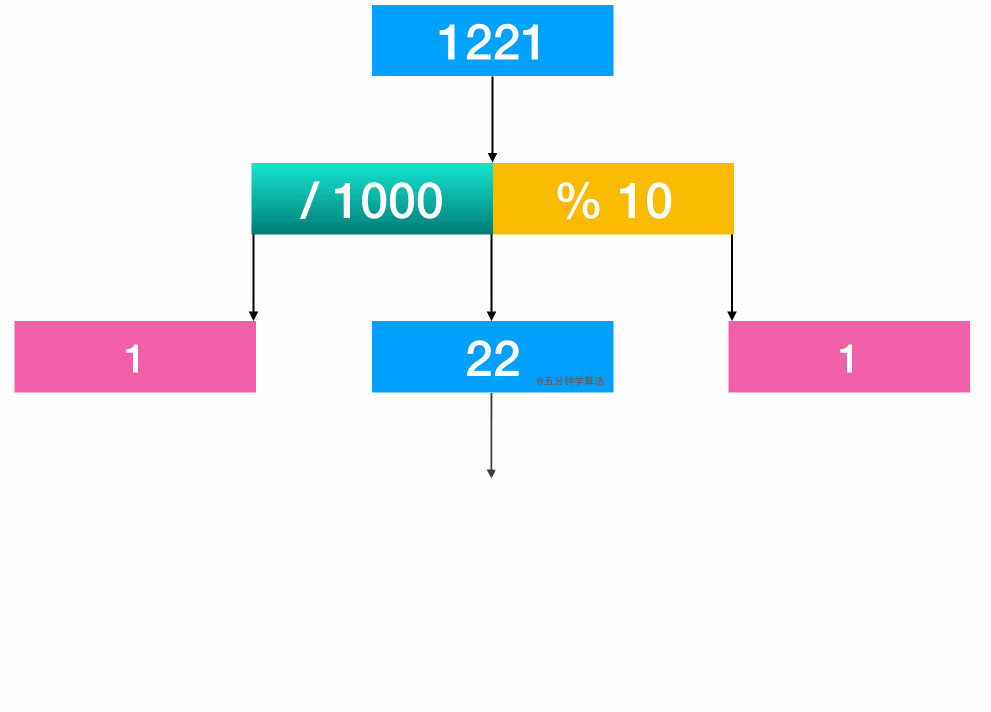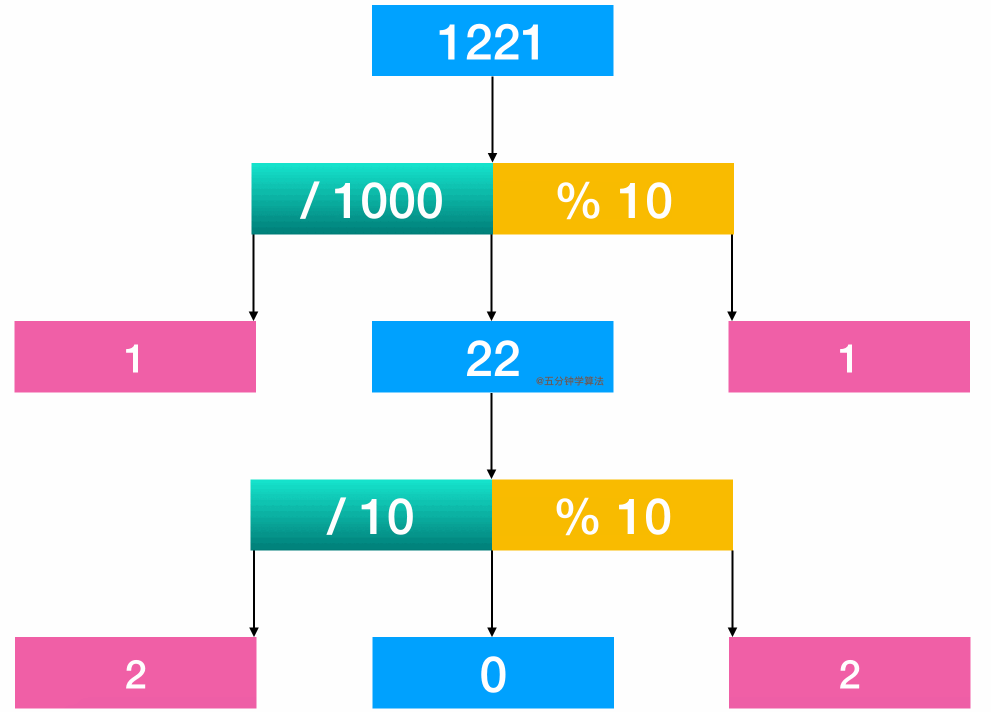
代码实现

class Solution:
    def isPalindrome(self, x: int) -> bool:
        if x<0:
            return False
        else:
            num_list = list(str(x))
            reverse = ''.join(num_list[::-1])
            if str(x) == reverse:
                return True
            else:
                return False

class Solution {
    public boolean isPalindrome(int x) {
        //边界判断
        if (x < 0) return false;
        int div = 1;
        //
        while (x / div >= 10) div *= 10;
        while (x > 0) {
            int left = x / div;
            int right = x % 10;
            if (left != right) return false;
            x = (x % div) / 10;
            div /= 100;
        }
        return true;
    }
}

二. 验证回文串

问题描述

给定一个字符串，验证它是否是回文串，只考虑字母和数字字符，可以忽略字母的大小写。

说明：本题中，我们将空字符串定义为有效的回文串。

示例 1:

输入: "A man, a plan, a canal: Panama"
输出: true

示例 2:

输入: "race a car"
输出: false

解题思路

在这道题中，我们的限定条件是只考虑字符串其中的字母和数字部分，并且字母大小写可忽略。我们可以使用双指针的方法，一个只指向开头字符，一个指向末尾字符，两指针所指字符分别比较。如果当前指针所指字符不是字母或数字，那么就越过这一字符，指向下一个字符，直到是字母或数字为止。这种双指针的方法，只需遍历一遍字符串即可判断。

代码实现

class Solution:
    def isPalindrome(self, s: str) -> bool:
        i, j = 0, len(s)-1
        while i < j :
            while i<j and not s[i].isalnum():
                i += 1
            while i<j and not s[j].isalnum():
                j -= 1
            if i < j :
                if s[i].lower() != s[j].lower():
                    return False
                i, j = i+1, j-1
        return True

复杂度分析

• 时间复杂度：O(|s|)，其中∣s∣ 是字符串s 的长度。
• 空间复杂度：O(1)。

三. 验证回文字符串Ⅱ

问题描述

给定一个非空字符串 s，最多删除一个字符。判断是否能成为回文字符串。

示例 1:

输入: "aba"
输出: True

示例 2:

输入: "abca"
输出: True
解释: 你可以删除c字符。

注意:

1. 字符串只包含从 a-z 的小写字母。字符串的最大长度是50000。

解题思路

考虑最朴素的方法：首先判断原串是否是回文串，如果是，就返回 true；如果不是，则枚举每一个位置作为被删除的位置，再判断剩下的字符串是否是回文串。这种做法的渐进时间复杂度是 O(n^2)的，会超出时间限制。

我们换一种想法。首先考虑如果不允许删除字符，如何判断一个字符串是否是回文串。常见的做法是使用双指针。定义左右指针，初始时分别指向字符串的第一个字符和最后一个字符，每次判断左右指针指向的字符是否相同，如果不相同，则不是回文串；如果相同，则将左右指针都往中间移动一位，直到左右指针相遇，则字符串是回文串。

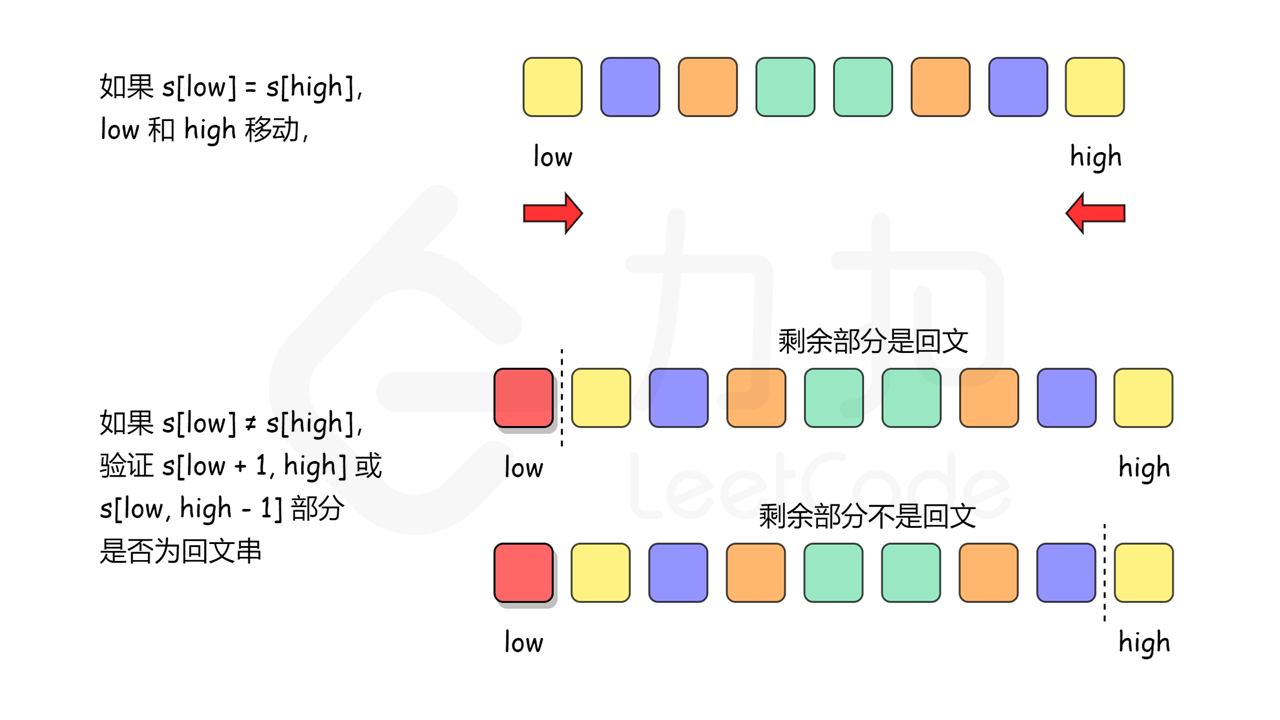
在允许最多删除一个字符的情况下，同样可以使用双指针，通过贪心算法实现。初始化两个指针 low 和 high 分别指向字符串的第一个字符和最后一个字符。每次判断两个指针指向的字符是否相同，如果相同，则更新指针，令 low = low + 1 和 high = high - 1，然后判断更新后的指针范围内的子串是否是回文字符串。如果两个指针指向的字符不同，则两个字符中必须有一个被删除，此时我们就分成两种情况：即删除左指针对应的字符，留下子串s[low + 1], ..., s[high]，或者删除右指针对应的字符，留下子串 s[low], s[low + 1], ..., s[high - 1]。当这两个子串中至少有一个是回文串时，就说明原始字符串删除一个字符之后就以成为回文串。

代码实现

class Solution:
    def validPalindrome(self, s: str) -> bool:
        def deletePalindrome(low, high):
            while low < high:
                if s[low] == s[high]:
                    low += 1
                    high -= 1
                else:
                    return False
            return True

        low, high = 0, len(s)-1
        while low<high:
            if s[low] == s[high]:
                low += 1
                high -= 1
            else:
                return deletePalindrome(low+1, high) or deletePalindrome(low, high-1)
        return True

四. 回文链表

问题描述

请判断一个链表是否为回文链表。

示例 1:

输入: 1->2
输出: false

示例 2:

输入: 1->2->2->1
输出: true

进阶：
你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题？

解题思路

第一步，我们需要遍历链表将值复制到数组列表中。我们用 currentNode 指向当前节点。每次迭代向数组添加 currentNode.val，并更新 currentNode = currentNode.next，当 currentNode = null 则停止循环。

执行第二部的最佳方法取决于你使用的变成语言。在 Python 中，很容易构造一个列表的反向副本，也很容易比较两个列表。在其他语言中，就没有那么简单。因此最好使用双指针法来检查是否为回文。我们在起点放置一个指针，在结尾放置一个指针，每一次迭代判断两个指针指向的元素是否相同，若不同，返回 false；相同则将两个指针向内移动，并继续判断，直到相遇。

在编码的过程中，注意我们比较的是节点值的大小，而不是节点本身。正确的比较方式是：node_1.val==node_2.val。而 node_1==node_2 是错误的。

代码实现

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def isPalindrome(self, head: ListNode) -> bool:
        listt = []
        while head:
            listt.append(head.val)
            head = head.next
        return listt == listt[::-1]

进阶解法

避免使用 O(n) 额外空间的方法就是改变输入。

我们可以将链表的后半部分反转（修改链表结构），然后将前半部分和后半部分进行比较。比较完成后我们应该将链表恢复原样。虽然不需要恢复也能通过测试用例，因为使用该函数的人不希望链表结构被更改。

算法：

我们可以分为以下几个步骤：

1. 找到前半部分链表的尾节点。

2. 反转后半部分链表。

3. 判断是否为回文。

4. 恢复链表。

5. 返回结果。

   执行步骤一，我们可以计算链表节点的数量，然后遍历链表找到前半部分的尾节点。

或者可以使用快慢指针在一次遍历中找到：慢指针一次走一步，快指针一次走两步，快慢指针同时出发。当快指针移动到链表的末尾时，慢指针到链表的中间。通过慢指针将链表分为两部分。

若链表有奇数个节点，则中间的节点应该看作是前半部分。

步骤二可以使用在反向链表问题中找到解决方法来反转链表的后半部分。

步骤三比较两个部分的值，当后半部分到达末尾则比较完成，可以忽略计数情况中的中间节点。

步骤四与步骤二使用的函数相同，再反转一次恢复链表本身。

class Solution:

    def isPalindrome(self, head: ListNode) -> bool:
        if head is None:
            return True

        # Find the end of first half and reverse second half.
        first_half_end = self.end_of_first_half(head)
        second_half_start = self.reverse_list(first_half_end.next)

        # Check whether or not there's a palindrome.
        result = True
        first_position = head
        second_position = second_half_start
        while result and second_position is not None:
            if first_position.val != second_position.val:
                result = False
            first_position = first_position.next
            second_position = second_position.next

        # Restore the list and return the result.
        first_half_end.next = self.reverse_list(second_half_start)
        return result    

    def end_of_first_half(self, head):
        fast = head
        slow = head
        while fast.next is not None and fast.next.next is not None:
            fast = fast.next.next
            slow = slow.next
        return slow

    def reverse_list(self, head):
        previous = None
        current = head
        while current is not None:
            next_node = current.next
            current.next = previous
            previous = current
            current = next_node
        return previous

反转链表使用的是头插法。

复杂度分析

• 时间复杂度：O(n)，其中 n 指的是链表的大小。
• 空间复杂度：O(1)，我们是一个接着一个的改变指针，我们在堆栈上的堆栈帧不超过 O(1)。
  该方法的缺点是，在并发环境下，函数运行时需要锁定其他线程或进程对链表的访问，因为在函数执执行过程中链表暂时断开。

总结

回文串问题是经典的初级算法，回顾这一文章，不难发现解决回文的问题追根溯源可以归结以下几种方法：

• 借助list反转实现判断
• 借助双指针，前后分别进行判断
• 链表借助list空间
• 求出回文的中间节点，将后一半的回文反转后，与前一半回文依次进行比较

参考

回文数

验证回文字符串 Ⅱ

回文链表