模拟求和问题

一. 二进制的加法

题目描述

给你两个二进制字符串，返回它们的和（用二进制表示）。

输入为 非空 字符串且只包含数字 1 和 0。

示例 1:

输入: a = "11", b = "1"
输出: "100"

示例 2:

输入: a = "1010", b = "1011"
输出: "10101"

 

提示：

  • 每个字符串仅由字符 '0' 或 '1' 组成。
  • 1 <= a.length, b.length <= 10^4
  • 字符串如果不是 "0" ，就都不含前导零。

解题思路

方法一： 转十进制相加

考虑一个最朴素的方法：先将a和b转化成十进制数，求和后再转化为二进制数。利用 Python 和 Java 自带的高精度运算，我们可以很简单地写出这个程序：

class Solution:
    def addBinary(self, a, b) -> str:
        return '{0:b}'.format(int(a, 2) + int(b, 2))

如果 a 的位数是 n，b 的位数为 m，这个算法的渐进时间复杂度为 O(n+m)。但是这里非常简单的实现基于 Python 和 Java 本身的高精度功能，在其他的语言中可能并不适用，并且在 Java 中：

  • 如果字符串超过 3333 位，不能转化为 Integer
  • 如果字符串超过 6565 位，不能转化为 Long
  • 如果字符串超过 500000001500000001 位，不能转化为 BigInteger

因此，为了适用于长度较大的字符串计算，我们应该使用更加健壮的算法。

方法二： 竖式模拟相加

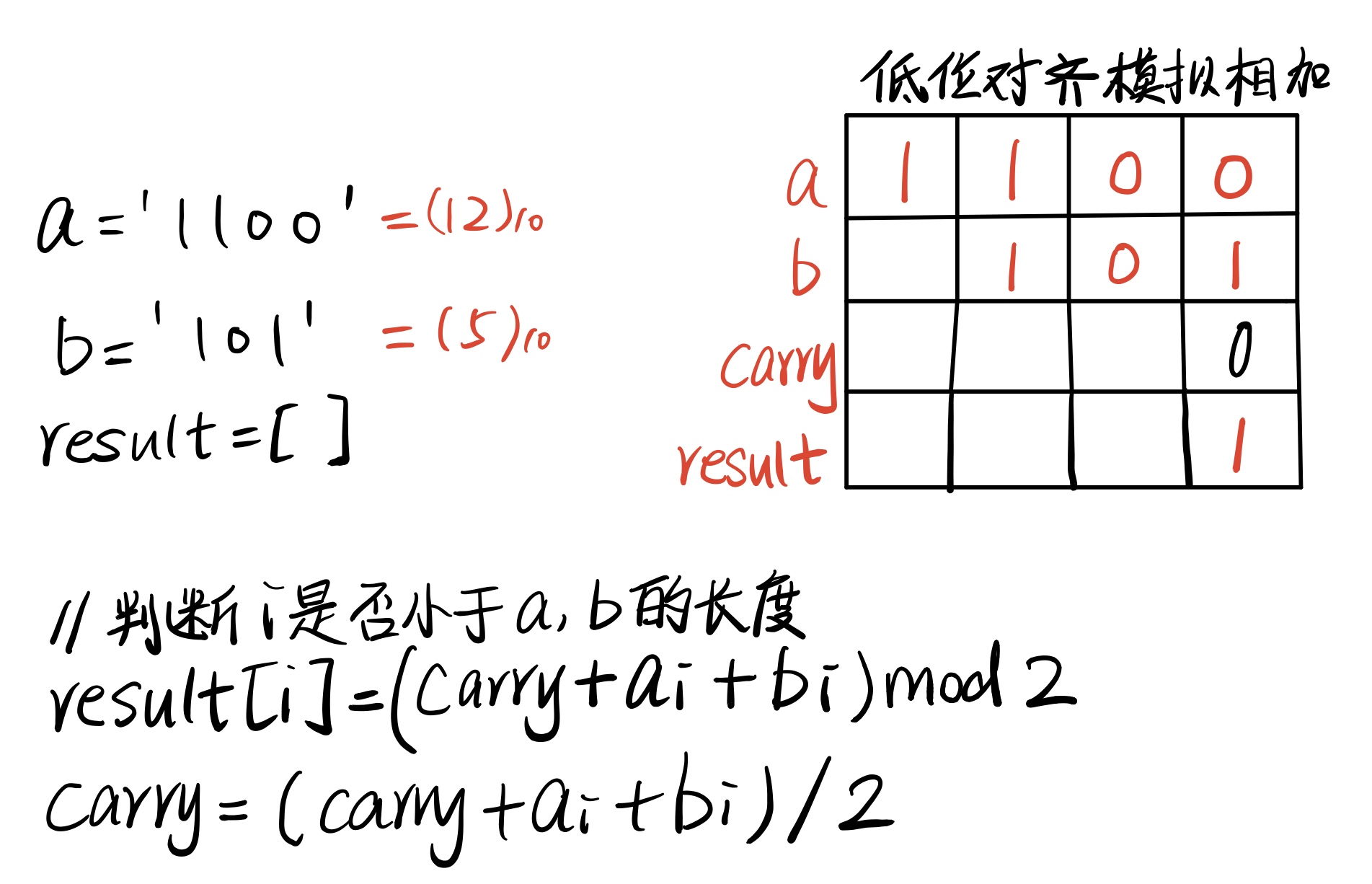
我们可以借鉴「列竖式」的方法，末尾对齐，逐位相加。在十进制的计算中「逢十进一」，二进制中我们需要「逢二进一」。

具体的，我们可以取
$$
n = max{ |a|, |b| }
$$
，循环 n 次，从最低位开始遍历。我们使用一个变量 carry 表示上一个位置的进位，初始值为 0。记当前位置对其的两个位为
$$
a^i,b^i
$$
，则每一位的答案为
$$
(carry + a^i+b^i)mod2
$$
，下一位的进位为
$$
⌊(carry + a^i+b^i)/2⌋
$$
。重复上述步骤，直到数字 a 和 b 的每一位计算完毕。最后如果 carry 的最高位不为 0，则将最高位添加到计算结果的末尾。

注意，为了让各个位置对齐，你也可以直接把 a 和 b 中短的那一个补 0 直到和长的那个一样长，然后从高位向低位遍历，对应位置的答案按照顺序存入答案字符串内，最终将答案串反转.

IMG_3114.jpg

代码实现

class Solution:
    def addBinary(self, a: str, b: str) -> str:
        results = []
        carry = 0
        for i in range(max(len(a), len(b))):
            carry += int(a[len(a) - i - 1]) if i < len(a) else 0
            carry += int(b[len(b) - i - 1]) if i < len(b) else 0
            results.append(str(carry % 2))
            carry //= 2
            i += 1
        if carry > 0 :
            results.append('1')
        return ''.join(results[::-1])

复杂度分析

假设 n=max{∣a∣,∣b∣}。

  • 时间复杂度：O(n)，这里的时间复杂度来源于顺序遍历 a 和 b。
  • 空间复杂度：O(1)，除去答案所占用的空间，这里使用了常数个临时变量。

二. 链表求和

题目描述

给定两个用链表表示的整数，每个节点包含一个数位。

这些数位是反向存放的，也就是个位排在链表首部。

编写函数对这两个整数求和，并用链表形式返回结果。

示例：

输入：(7 -> 1 -> 6) + (5 -> 9 -> 2)，即617 + 295
输出：2 -> 1 -> 9，即912

进阶：假设这些数位是正向存放的，请再做一遍。

示例：

输入：(6 -> 1 -> 7) + (2 -> 9 -> 5)，即617 + 295
输出：9 -> 1 -> 2，即912

解题思路

解题思路和上一题样，只不过这里增加了尾插法插入链表的操作。

代码实现

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
        end = results = ListNode(-1)
        carry = 0
        while l1 or l2:
            carry += l1.val if l1 else 0
            carry += l2.val if l2 else 0
            end.next = ListNode(carry % 10)
            end = end.next
            carry //= 10
            l1 = l1.next if l1 else None
            l2 = l2.next if l2 else None
        if carry >= 1:
            end.next = ListNode(1)
            end = end.next
        return results.next