题目描述

给定一个整数，写一个函数来判断它是否是 3 的幂次方。

示例 1:

输入: 27
输出: true

示例 2:

输入: 0
输出: false

示例 3:

输入: 9
输出: true

示例 4:

输入: 45
输出: false

进阶：
你能不使用循环或者递归来完成本题吗？

2和4的幂次问题同理

​ 对于求解幂次的问题，我们第一反应会是想到系统提供的库函数
$$
n = pow(x, y) \ 9 = pow(3, 2) \ 即3^2=9
$$
，那么最笨的方法就是使用这个库函数，设置一个计数变量i，表示幂次，然后依次计算pow，直到等于n为止。这种方法是时间复杂度最高的，也是计算量最大的方法，俗称‘笨’方法。我将在接下里的方法中介绍一种通用的求解幂问题的通用，较为快捷的方法，和针对一些特殊情况的小技巧方法。

解题思路

方法一：循环迭代

找出数字 n 是否是数字 b 的幂的一个简单方法是，n%3 只要余数为 0，就一直将 n 除以 b。

$$
n=b^x
$$

因此，应该可以将 n 除以 b x 次，每次都有 0 的余数，最终结果是 1。

class Solution:
    def isPowerOfThree(self, n: int) -> bool:
        if n < 1: return False
        while n % 3 == 0: n //= 3
        return n == 1

注意我们需要一个警卫来检查那个 n！=0，否则 while 循环将永远不会结束。对于负数，该算法没有意义，因此我们也将包括该保护。

复杂度分析

• 时间复杂度：O(log*b(n))，在我们的例子中是 O(\log n)*。除数是用对数表示的。

• 空间复杂度：O(1)，没有使用额外的空间。

这种做法同样适用2和4的幂次。

方法二：log运算法

我们可以用下面的数学公式，也就是高中所学的换底公式：
$$
n=3^i
$$

$$
i=log_3(n)={log_b(n)\over log_b(3)}
$$

若 n 是 3 的幂则 i 是整数。在 Java 中，我们通过取小数部分（利用 % 1）来检查数字是否是整数，并检查它是否是 0。

我们取b=10，进行换底计算，代码实现如下：

public class Solution {
    public boolean isPowerOfThree(int n) {
        return (Math.log10(n) / Math.log10(3)) % 1 == 0;
    }
}

其他编程语言的实现要看对应的API。

常见的陷阱 :
这个解决方案是有问题的，因为我们开始使用 double s，这意味着我们会遇到精度错误。说明在比较双精度数时不应使用 ==。这是因为 Math.log10(n)/Math.log10(3) 的结果可能是 5.0000001 或 4.9999999。使用 Math.log() 函数而不是Math.log10() 可以观察到这种效果。

为了解决这个问题，我们需要将结果与 epsilon 进行比较。

return (Math.log(n) / Math.log(3) + epsilon) % 1 <= 2 * epsilon;

复杂度分析

• 时间复杂度：Unknown。这里主要消耗时间的运算是 Math.log，它限制了我们算法的时间复杂性。实现依赖于我们使用的语言和编译器 。

• 空间复杂度： O(1)，我们没有使用任何额外的内存。epsilon 变量可以是内联的。

这种做法也同样适用2和4的幂次。

方法三：整数限制

这种解法的精髓就在于求出在编程语言中能够表示的最大的幂次结果，然后模上这个数n，如果结果为0，那么这个n就是幂次结果。

举例，比如在python中，整数所能表示的最大数是30。当然这只是个假设，为了方便理解！！！，那么在30之内最大的3的幂次就是27了。因为3*3*3=27，所以我直接用这个最大的27模上n，比如n=9。显然，若要使模后的结果为0，那么n必须也得是3的倍数，n=3, n=9。所以，直接用最大的能表示的幂次数直接模n，看看结果是否为0，就可以判断了。

那么问题是怎么找到这个在整数表示内的最大幂次数呢？
$$
MaxInt = \frac{ 2^{32} }{2} - 1
$$
因为我们使用 32 位来表示数字，所以范围的一半用于负数，0 是正数的一部分。

知道了 n 的限制，我们现在可以推断出 n 的最大值，也就是 3 的幂，是 1162261467。我们计算如下：
$$
3 ^{⌊log 3​ MaxInt⌋} =3^{⌊19.56⌋} =3^{19} =1162261467
$$

import math

class Solution:
    def isPowerOfThree(self, n: int) -> bool:
        maxInt = 2147483647 #python所能表达的最大正整数
        max_exp = pow(3, math.floor(math.log(maxInt, 3)))
        return n > 0 and max_exp % n == 0

复杂度分析

• 时间复杂度：O(1)。我们只做了一次操作。

• 空间复杂度： O(1)，没有使用额外空间。

这种方法只适用于底数为质数的数字，如3，5。

方法四：位运算（2为底）

该方法将通过位运算在 O(1) 的时间复杂度解决，通过使用如下的按位技巧：

• 如何获取二进制中最右边的 1：x & (-x)。

• 如何将二进制中最右边的 1 设置为 0：x & (x - 1)。

以下的两种解决方案背后的思想都是一样的：2 的幂在二进制中是有一个 1 后跟一些 0：
$$
1=(00000001) _2
$$

$$
2 = (0000 0010)_2
$$

$$
4 = (0000 0100)_2
$$

$$
8 = (0000 1000)_2
$$

不是 2 的幂的二进制中有一个以上的 1。
$$
3 = (00000011) _2
$$

$$
5 = (0000 0101)_2
$$

$$
6 = (0000 0110)_2
$$

$$
7 = (0000 0111)_2
$$

除了 0，我们应该单独处理。

获取最右边的 1

首先讨论为什么 x & (-x) 可以获取到二进制中最右边的 1，且其它位设置为 0。如下图所示：

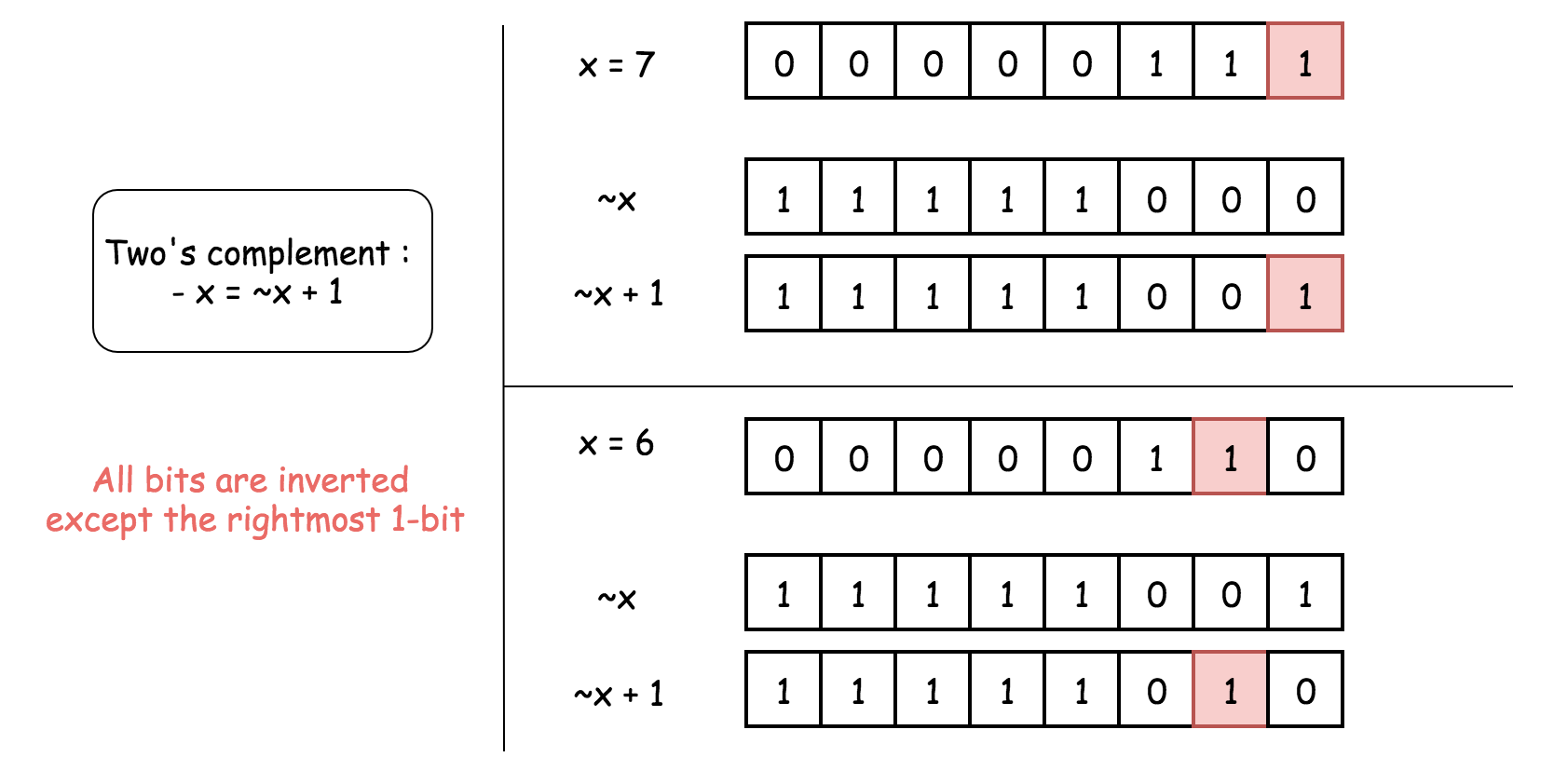
因此，x 和 −x 只有一个共同点：最右边的 1。这说明 x & (-x) 将保留最右边的 1。并将其他的位设置为 0。

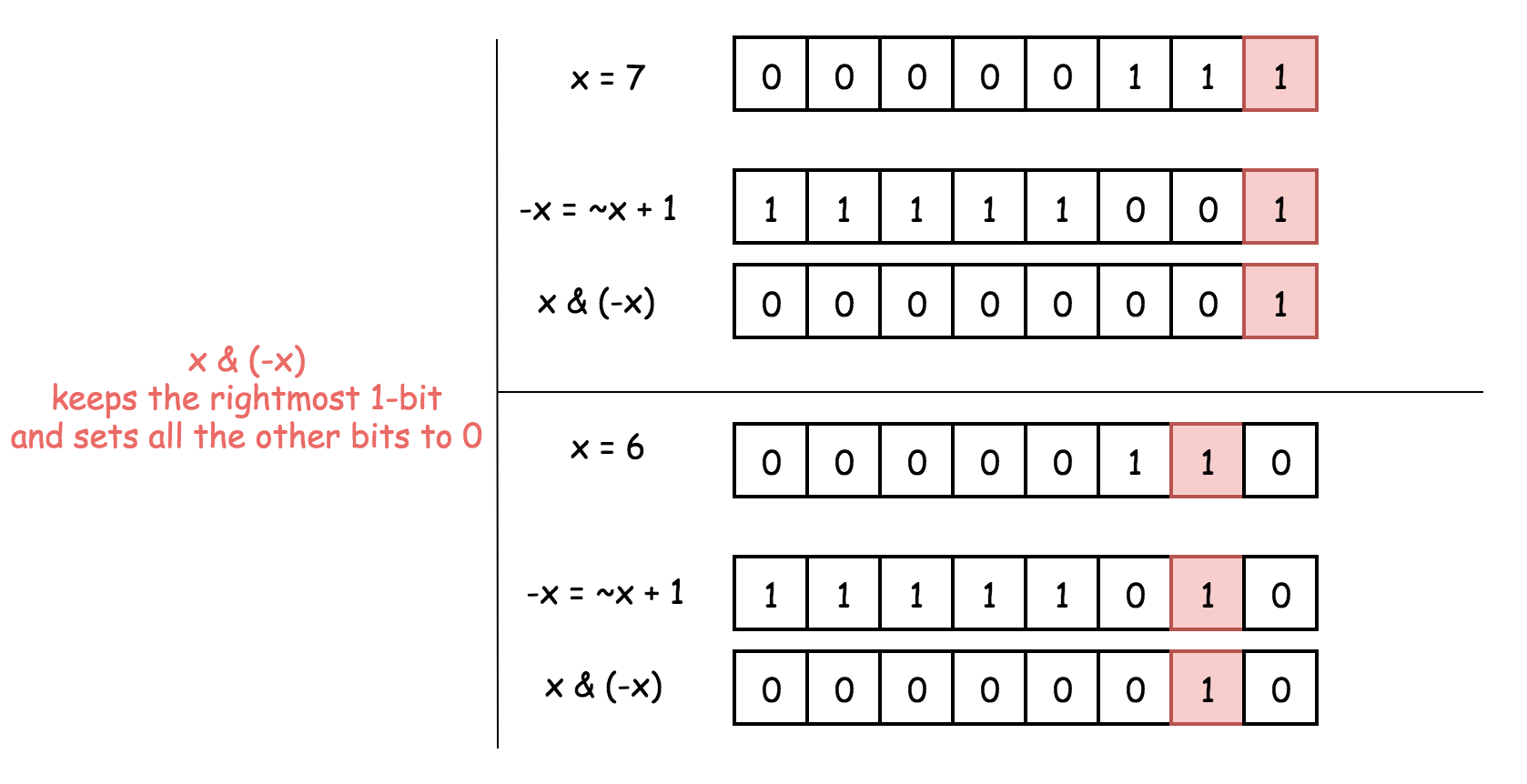
检测是否为 2 的幂：

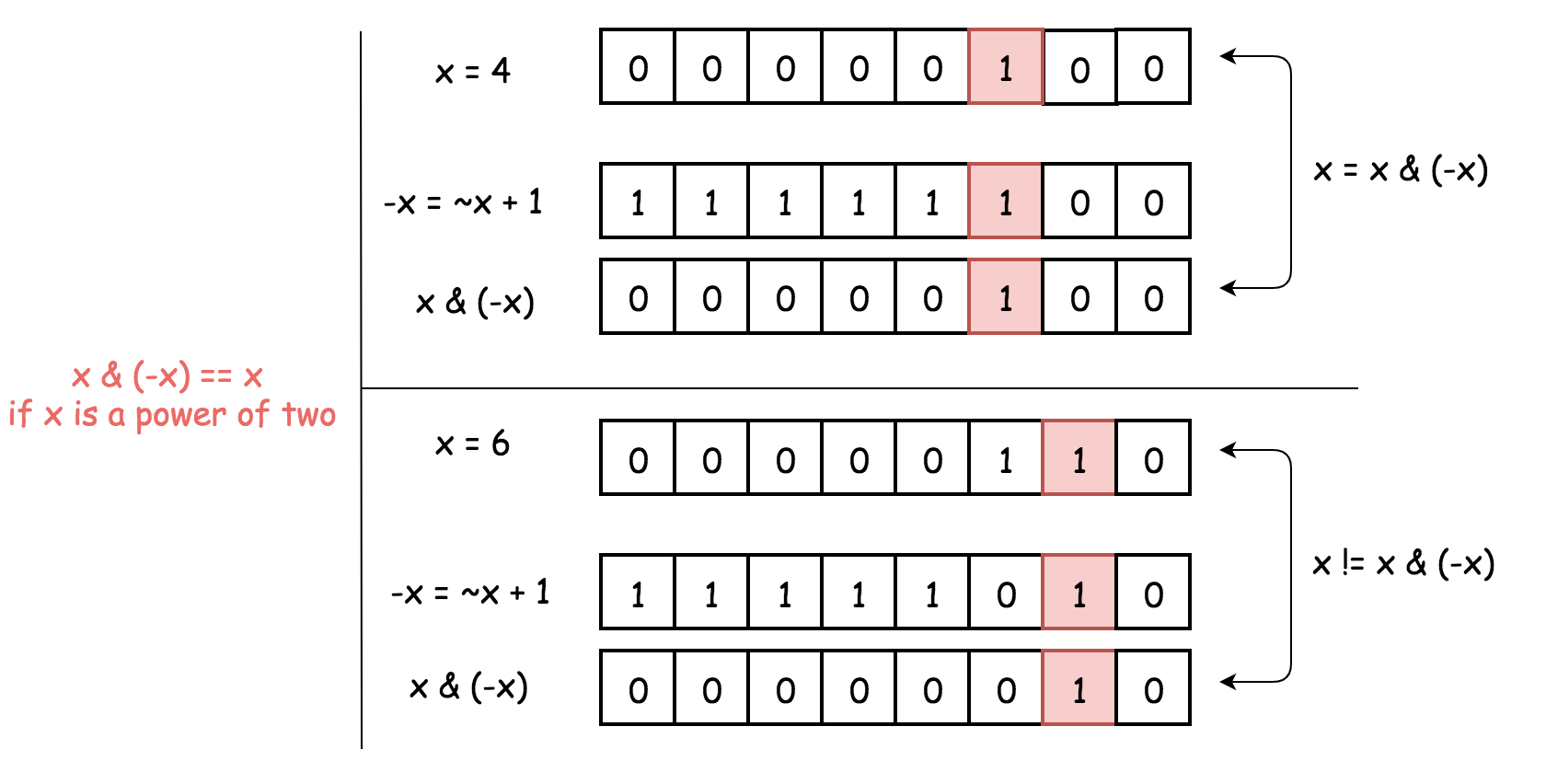
我们通过 x & (-x) 保留了最右边的 1，并将其他位设置为 0 若 x 为 2 的幂，则它的二进制表示中只包含一个 1，则有 x & (-x) = x。

若 x 不是 2 的幂，则在二进制表示中存在其他 1，因此 x & (-x) != x。

因此判断是否为 2 的幂的关键是：判断 x & (-x) == x。

class Solution(object):
    def isPowerOfTwo(self, n):
        if n == 0:
            return False
        return n & (-n) == n

复杂度分析

• 时间复杂度：O(1)。

• 空间复杂度：O(1)。

去除二进制中最右边的 1

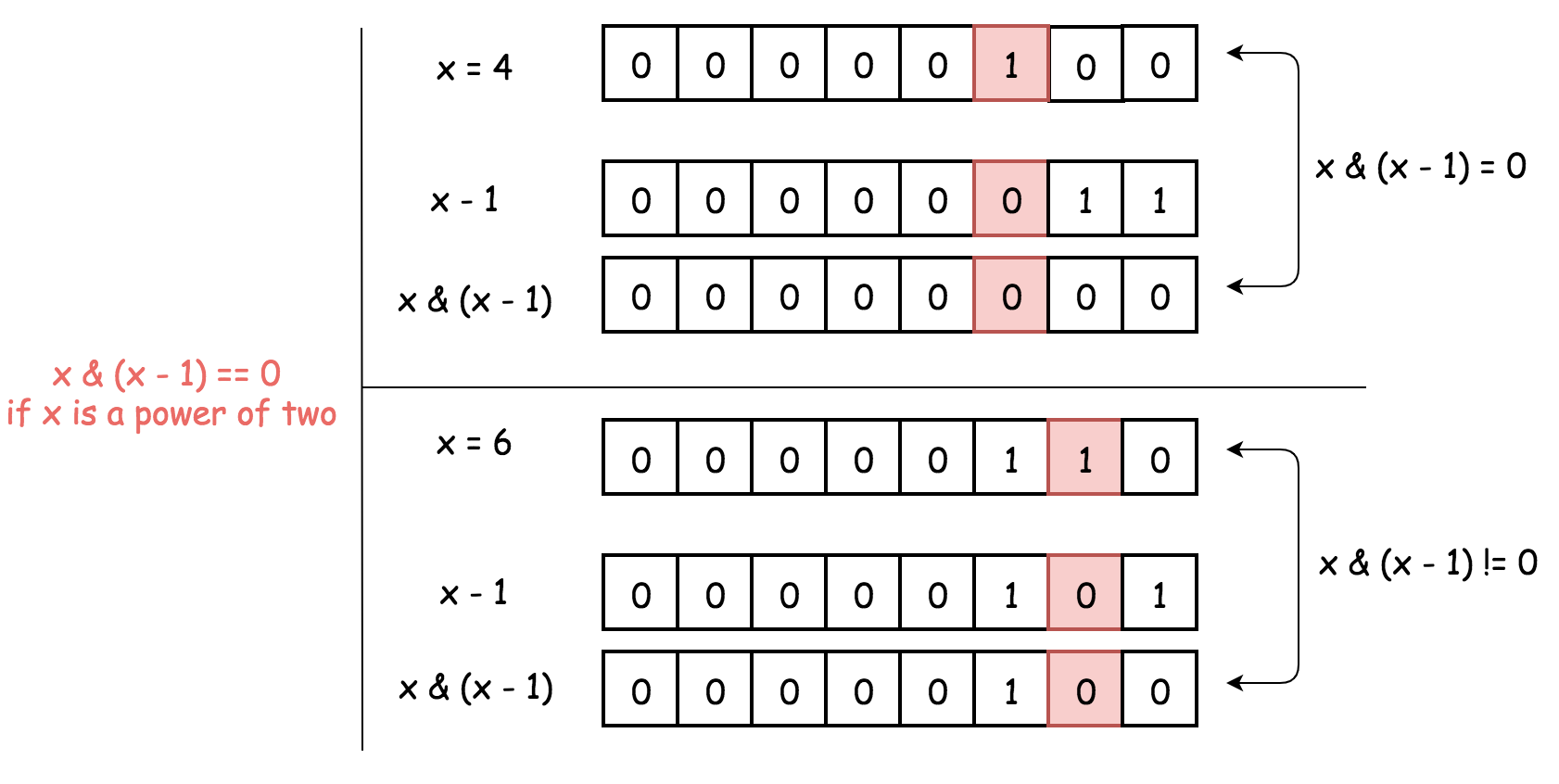
首先讨论为什么 x & (x - 1) 可以将最右边的 1 设置为 0。

(x - 1) 代表了将 x 最右边的 1 设置为 0，并且将较低位设置为 1。

再使用与运算：则 x 最右边的 1 和就会被设置为 0，因为 1 & 0 = 0。

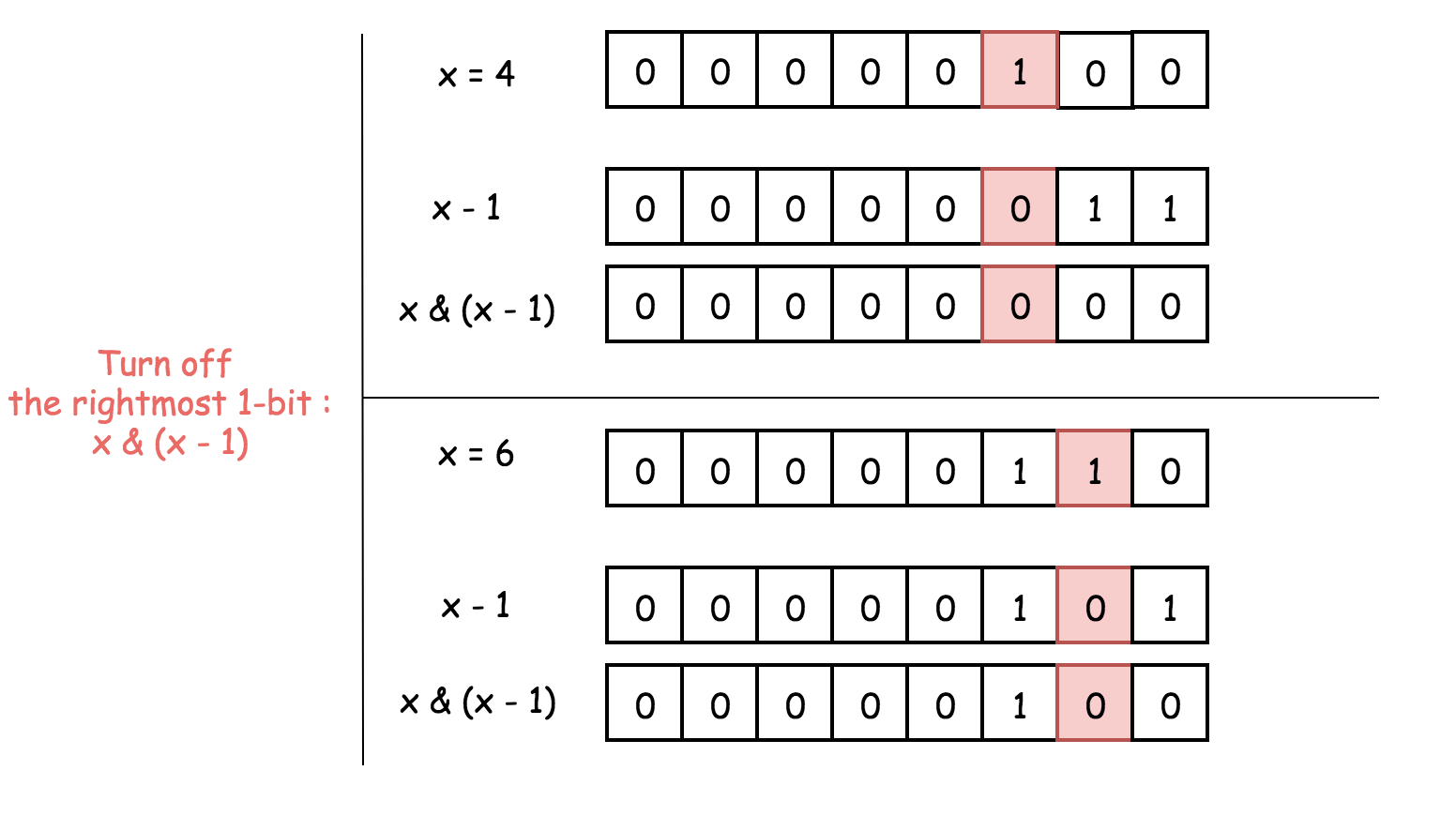
检测是否为 2 的幂：

• 2 的幂二进制表示只含有一个 1。

• x & (x - 1) 操作会将 2 的幂设置为 0，因此判断是否为 2 的幂是：判断 x & (x - 1) == 0。

class Solution(object):
    def isPowerOfTwo(self, n):
        if n == 0:
            return False
        return n & (n - 1) == 0

复杂度分析

• 时间复杂度：O(1)。

• 空间复杂度：O(1)。

这种方法只适用于底数为2或者4的数字

方法五：暴力破解法

我们提前计算所有可能答案。

我们知道输入的整数是 32 位整数
$$
x \le 2^{31} - 1
$$
因此我们最大 3的幂次为
$$
[\log_3\left(2^{31} - 1\right)] = 19
$$
那么我们总共有 20 种可能：
$$
3^0 , 3^1 , 3^2 , …, 3^{19}
$$
我们预计算全部可能，然后运行时检查输入数字是否在预计算列表中。

预计算：

result = []
for i in range(20):
    result.append(pow(3, i))

得到这样的一个列表：

[1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683, 59049, 177147, 531441, 1594323, 4782969, 14348907, 43046721, 129140163, 387420489, 1162261467]

然后判断n是否在列表中：

class Solution:
    def isPowerOfThree(self, n: int) -> bool:
        result = [1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683, 59049, 177147, 531441, 1594323, 4782969, 14348907, 43046721, 129140163, 387420489, 1162261467]
        return n in result

复杂度分析

• 时间复杂度：O(1)。

• 空间复杂度：O(1)。

这种方法适用于所有情况

方法六：位运算（4为底）

• 我们首先检查 num 是否为 2 的幂：x > 0 and x & (x - 1) == 0。

• 现在的问题是区分 2 的偶数幂（当 x 是 4 的幂时）和 2 的奇数幂（当 x 不是 4 的幂时）。在二进制表示中，这两种情况都只有一位为 1，其余为 0。

• 有什么区别？在第一种情况下（4 的幂），1 处于偶数位置：第 0 位、第 2 位、第 4 位等；在第二种情况下，1 处于奇数位置。

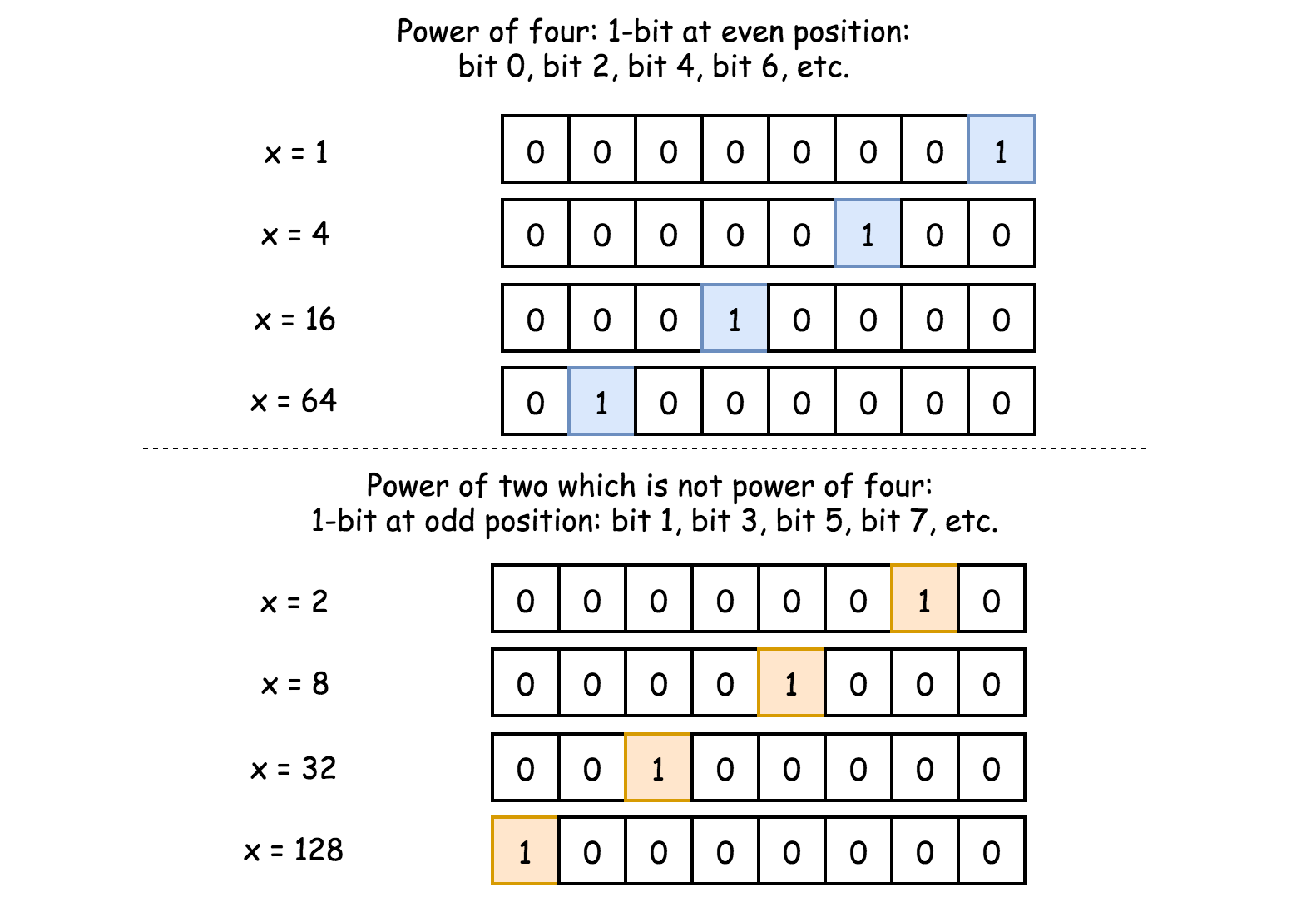
因此 4 的幂与数字
$$
(101010…10)_2
$$
相与会得到 0。即
$$
4^a \land (101010…10)_2 == 0
$$
(101010…10)2 用十六进制表示为 ：

$$
(aaaaaaaa)_{16}
$$

class Solution:
    def isPowerOfFour(self, n: int) -> bool:
        return n > 0 and n & (-n) == n and n & 0xaaaaaaaa == 0

复杂度分析

• 时间复杂度：O(1)。
• 空间复杂度：O(1)。

参考文章

4的幂

3的幂

2的幂