区间类问题有很多种：区间合并， 区间交集， 区间插入等等。 区间类问题只要的重难点就是找好区间直接重叠或不相交的条件。

题目描述

给出一个无重叠的 ，按照区间起始端点排序的区间列表。

在列表中插入一个新的区间，你需要确保列表中的区间仍然有序且不重叠（如果有必要的话，可以合并区间）。

 

示例 1：

输入：intervals = [[1,3],[6,9]], newInterval = [2,5]
输出：[[1,5],[6,9]]

示例 2：

输入：intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
输出：[[1,2],[3,10],[12,16]]
解释：这是因为新的区间 [4,8] 与 [3,5],[6,7],[8,10] 重叠。

 

解题思路

刚刚拿到这一题目，我的第一反应是想用之前解决区间问题的思路来解决这一问题。在这一题中，我们要新增一个区间，那么就会有两者插入情况：

1. 新插入的区间与原数组中的任何一个区间都不重叠，那么这个时候就要找出需要插入的位置；
2. 薪插入的区间与原数组中的某些区间有重叠，那么这个时候就要考虑区间合并的问题。

那么，这道题就好解了！设置好遍历区间和新增区间的三种位置关系，然后依次判断是否相交，然后按照区间合并的思路去做。

但是，当我真正用这种方法来套用这一题时，发现这么做的代码非常冗余，判断条件很多，稍不注意就会有遗漏的地方。归结到问题的本质还是要找出新区间与原区间的关系，确定好这个关系，问题就好解决了。

下面来介绍一种新的方法。

方法来源：

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/insert-interval/solution/cha-ru-qu-jian-by-leetcode-solution/
来源：力扣（LeetCode）

由于题目中的区间列表已经是按照区间起始排好序的，所以每一个区间的起始都大于前一个期间的起始。那么如果新加入的区间起始大于当前区间的结束，那么说明当前区间与新区间没有交集。那么可以遍历下一个区间了。

如果新加入的区间起始小于当前区间的结束，那么说明这两个区间是有交集的了，如下图所示：

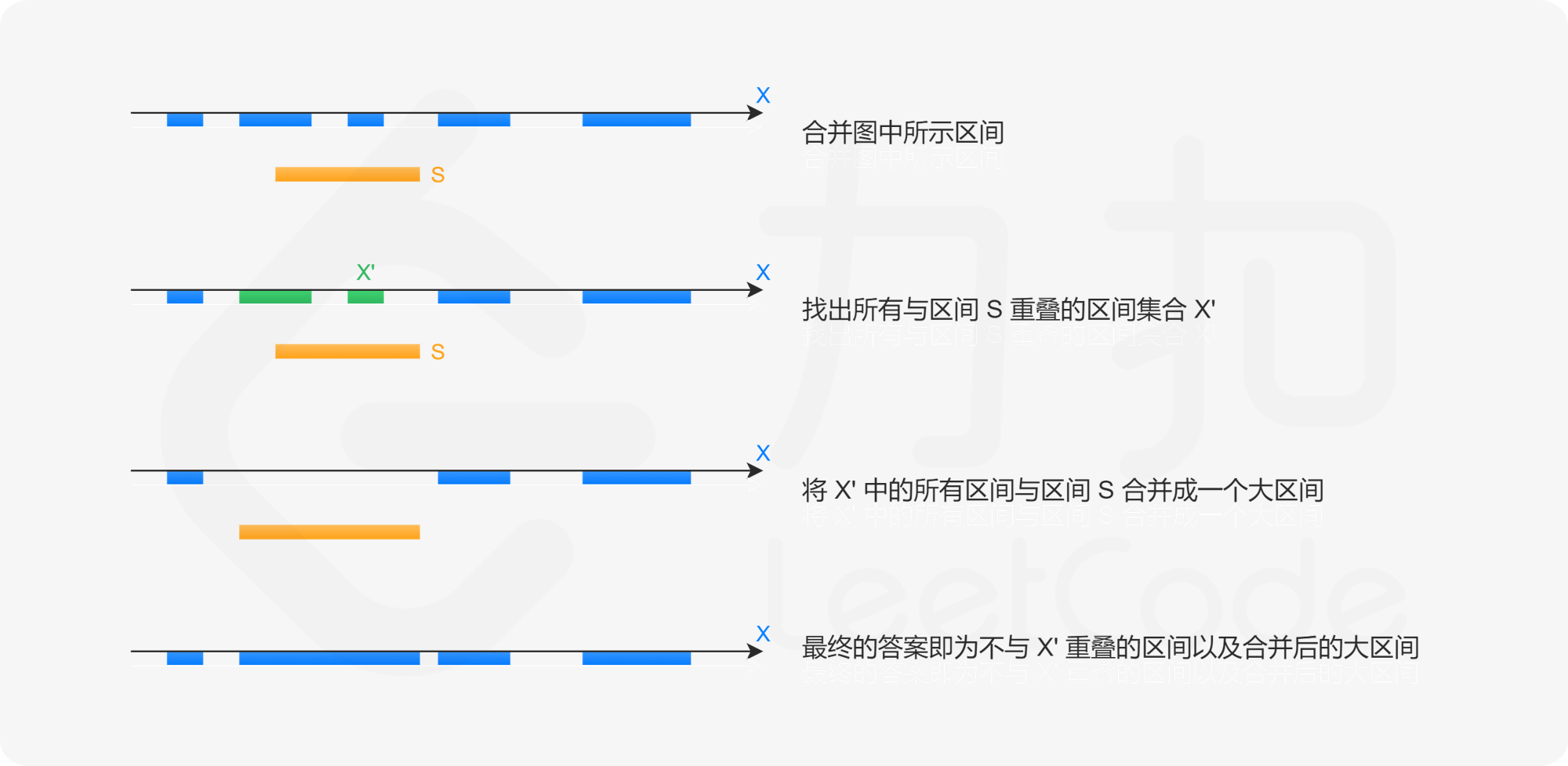
那么我们就要修改新插入区间的区间范围！！！

怎样修改？它们的交集即为：
$$
[min(l1, l2), min(r1, r2)]
$$
它们的并集为：
$$
[min(l1, l2), max(r1, r2)]
$$
那么直接就修改新插入的区间范围。

什么时候将新区间插入到区间列表中呢？当然是第一个满足新插入区间的结尾小于当前区间的起始的时候，说明它们两个无交集。这个时候就可以将新区间插入到列表中了！

代码实现

class Solution:
    def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:
        res = []
        remove = False
        left, right = newInterval
        for li, ri in intervals:
            # 新区间和当前区间无交集，直接将当前区间加到结果中
            if left > ri:
                res.append([li, ri])
            # 判断新区间是否要插入到列表中的条件
            elif li > right:
                if not remove:
                    res.append([left, right])
                    remove = True
                res.append([li, ri])
            # 新区间和当前区间有交集，进行新区间范围合并
            else:
                left = min(li, left)
                right = max(ri, right)

        if not remove:
            res.append([left, right])
        return res

复杂度分析

• 时间复杂度：O(n)，其中 n 是数组 intervals 的长度，即给定的区间个数。
• 空间复杂度：O(n)，除了存储返回答案的空间以外，我们只需要额外的常数空间即可。

其他方法

还可以不另外创造新的存储空间，直接对原列表进行原地修改。

从头到尾找到重叠的区间，记录重叠区间的索引，方便后续的切片替换。当区间不重叠的时候就可以直接替换掉重复的区间段了。

代码实现如下：

class Solution:
    def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:
        # 初始状况判断
        if not newInterval:
            return intervals
        if not intervals:
            return [newInterval]
        # 已经是起点有序的了
        i = 0
        intervalsLen = len(intervals)
        while i < intervalsLen and intervals[i][1] < newInterval[0]:
            i += 1
        # 保存删除之前的位置，最后在这个位置上插入
        tempI = i
        while i < intervalsLen and intervals[i][0] <= newInterval[1]:
            newInterval[0] = min(newInterval[0], intervals[i][0])
            newInterval[1] = max(newInterval[1], intervals[i][1])
            i += 1
        del intervals[tempI:i]
        intervals.insert(tempI, newInterval)
        return intervals