快速排序由于排序效率在同为O(N*logN)的几种排序方法中效率较高，因此经常被采用，再加上快速排序思想—-分治法也确实实用，因此很多软件公司的笔试面试，包括像腾讯，微软等知名IT公司都喜欢考这个，还有大大小的程序方面的考试如软考，考研中也常常出现快速排序的身影。

快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-Conquer Method)。

该方法的基本思想是：

1. 先从数组中取出一个数作为基准数。
2. 分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
3. 再对左右区间重复第二步，直到各区间只有一个数。

对于第一二步，就是我们所提到的partition操作。对于partition操作，有两种：

1 选取第一个元素作为中枢，进行partition

private int partition(int[] arr, int low, int high) {
    int i = low, j = high;
    int pivot = arr[i];
    while (i < j){
        while (i < j && arr[j] > pivot)
            j--;
        if (i < j) arr[i++] = arr[j];
        while (i < j && arr[i] < pivot)
            i++;
        if (i < j) arr[j--] = arr[i];
    }
    arr[i] = pivot;
    return i;
}

方法：i指向最左边的元素。j指向最右边的元素。i,j分别往中间移动。最后的位置就是pivot的位置！

2 选取最后一个元素作为中枢，进行partition

private int partition(int[] nums, int l, int r) {
    int pivot = nums[r];
    int i = l - 1;
    for (int j = l; j <= r - 1; ++j) {
        if (nums[j] <= pivot) {
            i = i + 1;
            swap(nums, i, j);
        }
    }
    swap(nums, i + 1, r);
    return i + 1;
}

方法：这种方法中分别用i的位置表示当前nums[i]的元素及之间的所有元素都小于nums[pivot]，nums[j]则表示大于nums[pivot]的最后一个元素的前一个元素。如图：

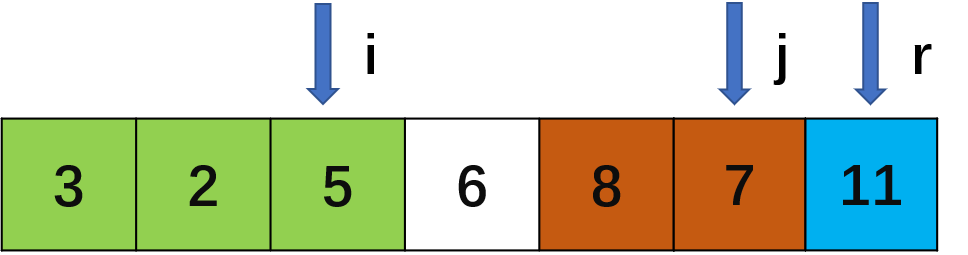
对于上一步的分区间完成之后，下面对于左右两个区间进行递归地排序

private void sort(int[] array, int low, int high) {
    if (low >= high)
        return;
    int mid = partition(array, low, high);
    sort(array, low, mid - 1);
    sort(array, mid + 1, high);
}

整合代码

class QuickSort {

    private boolean verbose;

    public QuickSort(boolean verbose) {
        this.verbose = verbose;
    }

    public void sort(int[] array) {
        int low = 0, high = array.length - 1;
        sort(array, low, high);
    }

    private void sort(int[] array, int low, int high) {
        if (low >= high)
            return;
        int mid = partition(array, low, high);
        sort(array, low, mid - 1);
        sort(array, mid + 1, high);
    }

    private int partition(int[] array, int low, int high) {
        // 挖坑 填坑的过程
        int pivot = array[low], i = low, j = high;
        while (i < j) {
            while (i < j && array[j] > pivot)
                j--;
            if (i < j) array[i++] = array[j];
            while (i < j && array[i] < pivot)
                i++;
            if (i < j) array[j--] = array[i];
        }
        array[i] = pivot;
        if (verbose) {
            System.out.println("array[pivot] = " + array[i]);
            for (int num : array) {
                System.out.print(" " + num);
            }
            System.out.println();
            ;
        }
        return i;
    }
}